Question 1192417: from the deck of 52 playing cards, how many ways can we choose 10 hearts and 10
diamonds?
Found 3 solutions by mananth, ikleyn, Edwin McCravy:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! The combination formula is:
C(n, r) = n! / (r! * (n-r)!)
Where n is the total r is the number we choose.
n = 26 (10 hearts and 10 diamonds) and r = 10.
C(26, 10) = 26! / (10! * (26-10)!)
= 10,400,600
10,400,600 ways to choose 10 hearts and 10 diamonds.
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
from the deck of 52 playing cards, how many ways can we choose 10 hearts and 10 diamonds?
~~~~~~~~~~~~~~~~~~~~
The solution by @mananth (note I do not call this person as a " tutor ")
is TOTALLY WRONG and FATALLY INCORRECT.
I came to bring you a correct solution.
A "standard" deck of playing cards consists of 52 Cards in each of the 4 suits
of Spades, Hearts, Diamonds, and Clubs. Each suit contains 13 cards:
Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King.
So, 10 hearts from 13 hearts can be chosen in 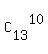 = 286 different ways.
10 diamonds can be chosen from 13 diamonds in = 286 different ways.
10 diamonds can be chosen from 13 diamonds in 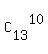 = 286 different ways.
These selections from different kinds of cards are independent.
Therefore, the total number of different selections the problem asks about is the product = 286 different ways.
These selections from different kinds of cards are independent.
Therefore, the total number of different selections the problem asks about is the product
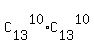 = 286*286 = 286^2 = 81796. ANSWER = 286*286 = 286^2 = 81796. ANSWER
Solved.
--------------------
Ignore the post by @mananth for your safety.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! from the deck of 52 playing cards, how many ways can we choose 10 hearts and 10
diamonds?
An alternate way of looking at the problem is to think of what is left behind
after selecting the hearts and diamonds. Think of this question:
After choosing the 10 hearts and 10 diamonds, how many ways can we be left with a
deck of only 32 cards, consisting of 26 black cards, 3 hearts and 3 diamonds?
We can choose the black cards only 1 way, the 3 hearts C(13,3)=286 ways, and the
3 diamonds C(13,3)=286 ways.
Answer = (1)(286)(286) = 81796 ways.
Edwin
|
|
|