|
Question 1192275: determine the point of the discontinuity of the rational function
2^2+7x-4/x^2+x-12
Found 3 solutions by ikleyn, josgarithmetic, greenestamps:
Answer by ikleyn(52848)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
determine the point of the discontinuity of the rational function
2^2+7x-4/x^2+x-12
~~~~~~~~~~~~~~~~~
I am 129% sure that the formula in your post is written incorrectly.
I mean, FATALLY incorrectly . . .
Double check it with your source and fix it if needed; then re-post to the forum.
Please do not post it to me personally.
/////////////
I don't know why @josgarithmetic appeared here with his guessing.
According to all the rules of decent and a common sense, he should not appear here with his hypotheses, at all.
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
You can put this solution on YOUR website! One could guess your expression really is (2^2+7x-4)/(x^2+x-12)
and numerator and denominator are the same as to mean 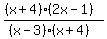 . .
The discontinuity is for x values giving 0 in the denominator factors, which are for x at -4.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
When you post a problem, it is polite to make sure you have written the problem correctly before you post it. It should not be necessary for us to guess what the problem is from your sloppy presentation.
Since the tutor who answered the question answered it incorrectly, I will respond to your post.
(1) I am sure that "2^2" in your function is supposed to be "2x^2".
(2) After correcting that, the function as you show it is 2x^2+7x-4/x^2+x-12 = 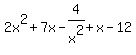 . Clearly that is not what you intended. If you are studying rational functions, then your mathematics education should have reached the point where you know that parentheses are important. The function you undoubtedly intended to show is (2x^2+7x-4)/(x^2+x-12) = . Clearly that is not what you intended. If you are studying rational functions, then your mathematics education should have reached the point where you know that parentheses are important. The function you undoubtedly intended to show is (2x^2+7x-4)/(x^2+x-12) = 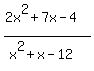
To find zeros, vertical asymptotes, and points of discontinuity, factor numerator and denominator:
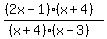
The factor (2x-1) in the numerator tells us there is a zero at x=1/2; the factor (x-3) in the denominator tells us there is a vertical asymptote at x=3.
The like factors (x+4) in both numerator and denominator tell us there is a discontinuity at x=-4. The given function is equivalent to the function 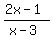 everywhere except when x=-4. everywhere except when x=-4.
At x=-4, the function 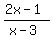 has the value has the value  , so the discontinuity is at the point (-4,9/7). , so the discontinuity is at the point (-4,9/7).
Here is a graph, showing the zero at x=1/2 and the vertical asymptote at x=3. The discontinuity at (-4,9/7) will not show up. If you graph this function on a good graphing calculator over a tiny interval between x=-4.1 and x=-3.9, you will see a hole in the graph.

|
|
|
| |