Question 1192250: Hotel A and B offers 2 types of packages that include lodging only or lodging with
breakfast. From a group of 300 tourists, 30 tourist choose Hotel A for lodging only and
120 tourists choose Hotel B for lodging with breakfast. Altogether 110 tourists choose to
stay in Hotel A. A tourist is selected randomly;
(a) What is the probability that the tourist chooses Hotel A or tourists chooses lodging only?
(b) What is the probability that the tourist to choose Hotel B for lodging with breakfast, if he chose Hotel B?
(c) What is the probability that the tourist to choose Hotel A, if he chose lodging without breakfast?
(d) What is the probability that the tourist chose Hotel A without breakfast or choose Hotel B with breakfast?
thank you in advance :)
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this probability problem:
First, let's organize the data into a table:
| Hotel | Lodging Only | Lodging with Breakfast | Total |
|---|---|---|---|
| A | 30 | 80 (110 total - 30 lodging only) | 110 |
| B | 90 (210 total - 120 with breakfast) | 120 | 210 |
| Total | 120 | 200 | 300 |
**(a) Probability of Hotel A or Lodging Only:**
P(A or Lodging Only) = P(A) + P(Lodging Only) - P(A and Lodging Only)
P(A) = 110/300
P(Lodging Only) = 120/300
P(A and Lodging Only) = 30/300
P(A or Lodging Only) = (110/300) + (120/300) - (30/300) = 200/300 = 2/3
**(b) Probability of Hotel B with Breakfast, given Hotel B:**
This is a conditional probability. We want P(B with Breakfast | B).
P(B with Breakfast | B) = P(B with Breakfast and B) / P(B)
Since "B with Breakfast" is a subset of "B", P(B with Breakfast and B) = P(B with Breakfast) = 120/300
P(B) = 210/300
P(B with Breakfast | B) = (120/300) / (210/300) = 120/210 = 4/7
**(c) Probability of Hotel A, given Lodging Only:**
This is also a conditional probability: P(A | Lodging Only)
P(A | Lodging Only) = P(A and Lodging Only) / P(Lodging Only)
P(A and Lodging Only) = 30/300
P(Lodging Only) = 120/300
P(A | Lodging Only) = (30/300) / (120/300) = 30/120 = 1/4
**(d) Probability of Hotel A without Breakfast or Hotel B with Breakfast:**
These are mutually exclusive events (they can't both happen at the same time), so we can simply add their probabilities.
P(A without Breakfast) = 30/300
P(B with Breakfast) = 120/300
P(A without Breakfast or B with Breakfast) = (30/300) + (120/300) = 150/300 = 1/2
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hotel A and B offers 2 types of packages that include lodging only or lodging with
breakfast. From a group of 300 tourists, 30 tourist choose Hotel A for lodging only
and 120 tourists choose Hotel B for lodging with breakfast.
Altogether 110 tourists choose to stay in Hotel A.
A tourist is selected randomly.
(a) What is the probability that the tourist chooses Hotel A or tourists chooses lodging only?
(b) What is the probability that the tourist to choose Hotel B for lodging with breakfast, if he chose Hotel B?
(c) What is the probability that the tourist to choose Hotel A, if he chose lodging without breakfast?
(d) What is the probability that the tourist chose Hotel A without breakfast or choose Hotel B with breakfast?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The key to solving this problem is to make a Table showing different categories in the hotels.
As soon as this table is complete, the rest is simple arithmetic.
In the post by @CPhill, the system, which calls himself as "Artificial Intelligence",
is not able to construct the table correctly and fails the solution in every section.
Below is my correct solution.
First, let's organize the data into a table:
Hotel Total Lodging Only Lodging with Breakfast
-----------------------------------------------------------------
A 110 (given) 30 (given) 110 - 30 = 80
B 300-110 = 190 190-120 = 70 120 (given)
**(a) Probability of Hotel A or Lodging Only:**
P(A or Lodging Only) = 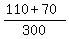 = = 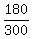 = =  = 0.6.
**(b) Probability of Hotel B with Breakfast, given Hotel B:**
This is a conditional probability
P(B with Breakfast | B) = = 0.6.
**(b) Probability of Hotel B with Breakfast, given Hotel B:**
This is a conditional probability
P(B with Breakfast | B) = 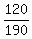 = =  .
**(c) Probability of Hotel A, given Lodging Only:**
This is also a conditional probability: P(A | Lodging Only)
P(A | Lodging Only) = .
**(c) Probability of Hotel A, given Lodging Only:**
This is also a conditional probability: P(A | Lodging Only)
P(A | Lodging Only) = 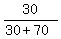 = = 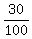 = =  = 0.3.
**(d) Probability of Hotel A without Breakfast or Hotel B with Breakfast:**
These are mutually exclusive events (they can't both happen at the same time), so we can simply add their probabilities.
P(A without Breakfast) + P(B with Breakfast) = = 0.3.
**(d) Probability of Hotel A without Breakfast or Hotel B with Breakfast:**
These are mutually exclusive events (they can't both happen at the same time), so we can simply add their probabilities.
P(A without Breakfast) + P(B with Breakfast) = 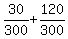 = =  = =  = 0.5. = 0.5.
At this point, the problem is solved completely.
--------------------------------------------------
I am very shocked to see the level of inaccuracy, demonstrated by this " AI ".
I also am very shocked by the style of presenting solution: it does not hesitate to produce wrong solution for simple problem,
shamelessly deceives the reader many times and its major goal is to make an impression to the reader how smart the AI is.
Is it what you call "the AI " ?
The score, which I give to this system today is the hard " 2 " in the 5-score scale.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|