SOLUTION: the parabola y=2x^2 is translated to a new parabola with x intercepts 4 and -3. The y-intercept of the new parabola is a.12 b.-12 c.-0.5 d.-24

Translations of a parabola do not change the coefficient at x^2.


From the other side, the symmetry line of the new parabola is  x = 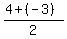 = 0.5


Therefore, the new parabola is  y = 2*(x-0.5)^2 + b, where b is an unknown value.


To find "b", use the condition that x-intercept is 4:

    y = 0 = 2*(x-0.5)^2 + b  at  x= 4,

or

    0 = 2*(4-0.5)^2 + b,

    0 = 2*3.5^2 + b

    0 = 24.5 + b

    b = - 24.5.


Thus the new parabola is  y = 2*(x-0.5)^2 - 24.5,  and its value at x= 0 is

y = 2*(0-0.5)^2 - 24.5 = 2*0.5^2 - 24.5 = -24.    ANSWER

Since the new parabola has x-intercepts 4 and -3, the new quadratic function has the form

    y = a*(x+3)*(x-4)


With some real coefficient "a".


Since translations leave the leading coefficient at x^2 unchangeable, a = 2.


It implies that the new quadratic function is  y = 2*(x+3)*(x-4).


Therefore, y-intercept of the new parabola is y(0) = 2*(0+3)*(0-4) = 2*3*(-4) = -24.    ANSWER