Question 1192052: Triplets Peter, Reeta and Nikita have two ways for getting home from school each day: cycle on a tandem bike or walk. The bike can carry either one or two riders at a time. Regardless of the number of people pedalling, cycling speed is 5 times walking speed. The triplets always leave school at the same time and always use the same path between school and home, whether walking or cycling. The school is 5 km from home and their walking speed is 4 kilometres per hour.
a) On Monday, Nikita and Peter cycle and Reeta walks. On reaching the point four-fifths of the way home the bike gets a puncture, so Nikita and Peter walk the rest of the way home. How far from school is Peeta when the cyclists arrive home?
b) On Tuesday, Peter and Reeta ride the bike and Nikita walks. When the cyclists arrive home, Peter hops off the bike and Reeta rides back towards school to collect Nikita. How far from school is Nikita when Reeta reaches her?
c) On Wednesday, Reeta and Nikita take the bike and Peter walks. When the cyclists are halfway home, Reeta hops off and walks the rest of the way, while Nikita heads back to pick up Peter. How far from school is Reeta when her siblings pass her on the bike?
d) On Thursday, it is Reeta's turn to walk. Peter drops Nikita off at a certain point leaving her to walk home. Meanwhile he returns to pick up Reeta and they cycle home together. If all three arrive home at the same time, how far from school are the drop-off and pick-up points?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**a) Monday:**
1. **Walking speed:** 4 km/h
2. **Cycling speed:** 4 km/h * 5 = 20 km/h
3. **Distance cycled:** (4/5) * 5 km = 4 km
4. **Time taken to cycle:** 4 km / 20 km/h = 0.2 hours
5. **Distance walked by Reeta:** 4 km/h * 0.2 hours = 0.8 km
6. **Distance remaining for Reeta:** 5 km - 0.8 km = 4.2 km
7. **Time taken to walk the remaining distance:** 4.2 km / 4 km/h = 1.05 hours
8. **Total time taken by cyclists (and Reeta):** 0.2 hours + 1.05 hours = 1.25 hours
9. **Distance walked by Reeta in total:** 4 km/h * 1.25 hours= 5km
10. **When the cyclists arrive home, Reeta is already home.**
**b) Tuesday:**
1. **Time taken by cyclists to reach home:** 5 km / 20 km/h = 0.25 hours
2. **Distance walked by Nikita:** 4 km/h * 0.25 hours = 1 km
3. **Distance remaining for Nikita:** 5 km - 1 km = 4 km
4. **Time taken by Reeta to cycle back to collect Nikita:** Let 't' be the time. Reeta cycles 20t km and Nikita walks 4t km. The distance they cover together must equal the remaining distance of Nikita. So, 20t + 4t = 4 => t = 4/24=1/6 hours
5. **Distance covered by Nikita during this time:** 4 km/h * (1/6) hours = 2/3 km
6. **Total distance walked by Nikita:** 1 km + (2/3) km = 5/3 km
7. **Distance from school when Reeta reaches her:** 5 km - (5/3) km = 10/3 km = 3.33 km
**c) Wednesday:**
1. **Time taken by cyclists to reach halfway point:** 2.5 km / 20 km/h = 0.125 hours
2. **Distance walked by Peter:** 4 km/h * 0.125 hours = 0.5 km
3. **Distance remaining for Peter:** 5 km - 0.5 km = 4.5 km
4. **Let 't' be the time taken for Nikita to cycle back and meet Peter.** Nikita cycles 20t and Peter walks 4t. The combined distance covered by both must equal the remaining distance of Peter. So, 20t + 4t = 4.5 => t = 4.5/24 = 3/16 hours.
5. **Distance walked by Reeta after hopping off:** 4 km/h * (3/16) hours = 0.75 km
6. **Distance from school when siblings meet Reeta:** 2.5 km + 0.75 km = 3.25 km
**d) Thursday:**
1. Let 'x' be the distance from school where Nikita is dropped off.
2. Time taken by Nikita to walk home: (5-x) / 4
3. Time taken by Peter to drop Nikita and return to collect Reeta: 2x / 20 = x/10
4. Reeta walks (5-x) km. Time taken by Reeta to walk the remaining distance= (5-x)/4
5. Peter and Reeta cycle the remaining distance. The remaining distance is 5-x km. The time taken by Peter and Reeta to cycle = (5-x)/20
6. Since all arrive home at the same time: (5-x)/4 = x/10 + (5-x)/20
7. Multiplying by 20, we get: 5(5-x) = 2x + (5-x) => 25 - 5x = x + 5 => 20 = 6x => x = 10/3 km = 3.33 km
Drop-off and pick-up points are 3.33 km from school.
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Triplets Peter, Reeta and Nikita have two ways for getting home from school each day: cycle on a tandem bike or walk.
The bike can carry either one or two riders at a time.
Regardless of the number of people pedalling, cycling speed is 5 times walking speed.
The triplets always leave school at the same time and always use the same path between school and home,
whether walking or cycling. The school is 5 km from home and their walking speed is 4 kilometres per hour.
a) On Monday, Nikita and Peter cycle and Reeta walks. On reaching the point four-fifths of the way home
the bike gets a puncture, so Nikita and Peter walk the rest of the way home. How far from school is Peeta when the cyclists arrive home?
b) On Tuesday, Peter and Reeta ride the bike and Nikita walks. When the cyclists arrive home,
Peter hops off the bike and Reeta rides back towards school to collect Nikita. How far from school is Nikita when Reeta reaches her?
c) On Wednesday, Reeta and Nikita take the bike and Peter walks. When the cyclists are halfway home,
Reeta hops off and walks the rest of the way, while Nikita heads back to pick up Peter.
How far from school is Reeta when her siblings pass her on the bike?
d) On Thursday, it is Reeta's turn to walk. Peter drops Nikita off at a certain point leaving her to walk home.
Meanwhile he returns to pick up Reeta and they cycle home together. If all three arrive home at the same time,
how far from school are the drop-off and pick-up points?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the solution by @CPhill to this problem, his interpretation for part (d) is CERTAINLY incorrect.
The correct interpretation for part (d), from the problem, is that first Peter and Nikita are cycling,
while Reeta is  - - - not waiting at the school. - - - not waiting at the school.
Then Peter drops Nikita off at a certain point leaving her to walk home, and Peter returns back
to pick up Reeta on her way to the home.
After that, Peter and Reeta are cycling home together.
It is the ONLY one and the UNIQUE possible interpretation, and the text points it directly, saying in (d) that
" On Thursday, it is Reeta's turn to walk ".
It is a classic Travel and Distance problem, which I know along and across from my school years.
So, below is my solution for part (d) in this correct interpretation.
So, the distance from the school to home is 5 km; walking speed is 4 km/h and the cycling speed is 20 km/h.
Let x be the distance from the school to the drop-off point and
let y be the distance from the school to the pick-up point.
The time for Peter to get the drop-off point is  hours.
The time for Peter to move from the drop-off point to pick-up point is hours.
The time for Peter to move from the drop-off point to pick-up point is  hours.
The time for Peter to get the drop-off point and then to return to the pick-up point is the sum hours.
The time for Peter to get the drop-off point and then to return to the pick-up point is the sum
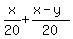 = =  . (1)
This time, . (1)
This time,  hours, is equal to the time for Reeta to get the pick-up pont from the school, which is hours, is equal to the time for Reeta to get the pick-up pont from the school, which is 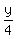 hours.
It gives us this equation hours.
It gives us this equation
 = = 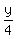 . (2)
Simplify it
4(2x-y) = 20y, or 2x-y = 5y, or 2x = 5y + y, or 2x = 6y, or x = 3y. (3).
+------------------------------------------------------------------------+
| At this point, we complete our consideration for moving Peter |
| from the school to the drop-off point and then to the pick-up point. |
+------------------------------------------------------------------------+
Now we will consider the other part of moving.
The time for Nikita to get the home from the drop-off point walking is . (2)
Simplify it
4(2x-y) = 20y, or 2x-y = 5y, or 2x = 5y + y, or 2x = 6y, or x = 3y. (3).
+------------------------------------------------------------------------+
| At this point, we complete our consideration for moving Peter |
| from the school to the drop-off point and then to the pick-up point. |
+------------------------------------------------------------------------+
Now we will consider the other part of moving.
The time for Nikita to get the home from the drop-off point walking is  hours.
During this time, Peter is cycling from point x to point y and then from point y to the home.
It takes for Peter hours.
During this time, Peter is cycling from point x to point y and then from point y to the home.
It takes for Peter  + +  = =  hours.
The time hours.
The time  for Nikita is the same as the time for Nikita is the same as the time  for Peter.
It gives us this equation for Peter.
It gives us this equation
 = =  . (4)
Simplify it
20(5-x) = 4(5+x- 2y), or 100-20x = 20+4x-8y, or 100-20 = 4x + 20x-8y, or 24x-8y = 80, or 3x - y = 10. (5)
Thus, we have now two equations
x = 3y and 3x - y = 10.
Substitute first equation, x = 3y, into the second equation
3*(3y) - y = 10, or 9y - y = 10, 8y = 10, y = . (4)
Simplify it
20(5-x) = 4(5+x- 2y), or 100-20x = 20+4x-8y, or 100-20 = 4x + 20x-8y, or 24x-8y = 80, or 3x - y = 10. (5)
Thus, we have now two equations
x = 3y and 3x - y = 10.
Substitute first equation, x = 3y, into the second equation
3*(3y) - y = 10, or 9y - y = 10, 8y = 10, y = 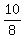 = =  = 1.25.
Then x = 3y = 3*1.25 = 3.75.
Thus the drop-off point is 3.75 km from the school, and the pick-up point is 1.25 km from the school. ANSWER = 1.25.
Then x = 3y = 3*1.25 = 3.75.
Thus the drop-off point is 3.75 km from the school, and the pick-up point is 1.25 km from the school. ANSWER
At this point, the part (d) of the problem is solved completely.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|