|
Question 1191931: Find the equation of a circle tangent to the line 3x - 4y = 34 at the point (10, -1) and also
tangent to the line 4x + 3y = 12 at the point (3, 0).
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of a circle tangent to the line 3x - 4y = 34 at the point (10, -1) and also
tangent to the line 4x + 3y = 12 at the point (3,0).
-------------------------
Find the perpendicular bisectors of the 2 lines at the given points.
The intersection of the bisectors is the center of the circle at (h,k).
Find the distance from the center to either point, that's the radius, r.
 is the circle. is the circle.
----------------------------
Email via the TY note for help or to check your work.
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the equation of a circle tangent to the line 3x - 4y = 34 at the point (10, -1) and also
tangent to the line 4x + 3y = 12 at the point (3, 0).
~~~~~~~~~~~~~~~~~~
This problem is NOT an ORDINARY problem : it is a SPECIAL.
It is a special, since it is OVER-DEFINED.
It is clear that the center of the circle lies at the intersection of perpendicular lines to the given lines
at the given points;
but when we will find this intersection, we should CHECK that the distance is the same from the intersection
point to both given points.
So I came to assist you in making all necessary steps.
(1) The line perpendicular to 3x - 4y = 34 is 4x + 3y = const (you swap x and y and change the sign in the left side at one term).
In order for the point (10,-1) would belong to this perpendicular line, the const must be const = 4*10 + 3*(-1) = 40 - 3 = 37.
So, first perpendicular line is 4x + 3y = 37.
(2) The line perpendicular to 4x + 3y = 12 is 3x - 4y = const (you swap x and y and change the sign in the left side at one term).
In order for the point (3,0) would belong to this perpendicular line, the const must be const = 3*3 - 4*0 = 9 - 0 = 9.
So, second perpendicular line is 3x - 4y = 9.
(3) To find the intersection point, you should solve this system of two equations
4x + 3y = 37 (1)
3x - 4y = 9 (2)
The intersection point is (by the determinant method)
x = 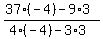 = 7; y = = 7; y = 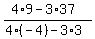 = 3.
(4) So, the intersection point and the center of the circle is the point (x,y) = (7,3).
The distance to the point (10,-1) is = 3.
(4) So, the intersection point and the center of the circle is the point (x,y) = (7,3).
The distance to the point (10,-1) is 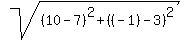 = = 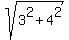 = =  = 5.
The distance to the point (3,0) is = 5.
The distance to the point (3,0) is  = = 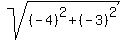 = =  = 5.
(5) The distances are the same, so the problem is posed correctly.
(6) The standard form equation of the circle is = 5.
(5) The distances are the same, so the problem is posed correctly.
(6) The standard form equation of the circle is 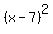 + + 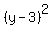 = =  . .
Solved.
|
|
|
| |