Let the integral that we wish to integrate be I


 Which factor, if either, is harder to integrate?
I'd say sin(4x) is harder to integrate, so let it be u.
Which factor, if either, is harder to integrate?
I'd say sin(4x) is harder to integrate, so let it be u.






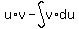

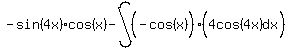

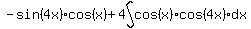 So let's write and mark what we have so far, so we can come back to
it and substitute:
-----------------------------------------------------------
So let's write and mark what we have so far, so we can come back to
it and substitute:
-----------------------------------------------------------


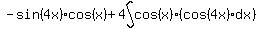 -----------------------------------------------------------
We now have find
-----------------------------------------------------------
We now have find 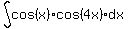 But we have to be careful here, so we don't "undo" what we just did.
For this part, be sure to let u equal to the part that came from
what we let u equal before.
But we have to be careful here, so we don't "undo" what we just did.
For this part, be sure to let u equal to the part that came from
what we let u equal before.




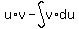



 Let's write what we have here.
Let's write what we have here.


 That integral on the right is just the original integral that we called I:
That integral on the right is just the original integral that we called I:


 So we go back to
So we go back to


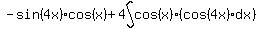 and substitute cos(4x)sin(x)+4I for the last integral:
and substitute cos(4x)sin(x)+4I for the last integral:





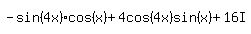 Now we solve for I
Now we solve for I


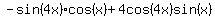


 But don't forget to put +C on the end.
[It isn't necessary to put +C in the integration steps.]
But don't forget to put +C on the end.
[It isn't necessary to put +C in the integration steps.]


 Edwin
Edwin