Question 1191739: Graph the inequalities y>=|x-2| and y<=4-|x|. What is the area of the enclosed region?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is some graphs:
(1) The basic function |x|
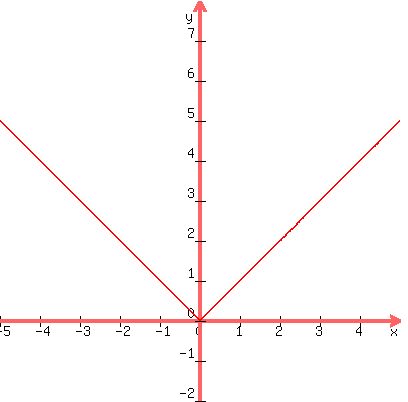
(2) The graph of |x-2|: the basic graph shifted 2 to the right

(3) The graph of 4-|x|, which is the same as -|x|+4: the basic graph flipped vertically and translated up 4
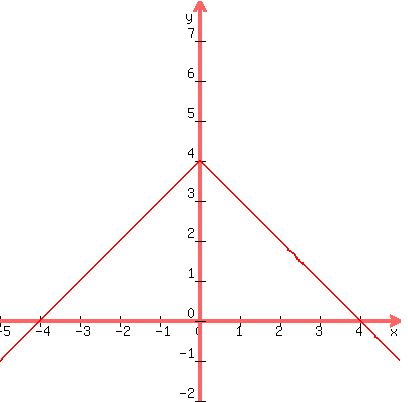
The two given functions, graphed together:
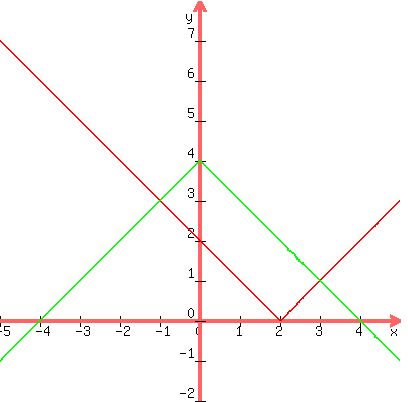
The coefficients of x in both functions are 1, so all the line segments in the graph of each function have slopes of 1 or -1; so the area between the graphs is a rectangle.
Clearly two of the vertices of that rectangle are (0,4) and (2,0).
It appears from the graph that the other two corners are (-1,3) and (3,1); substituting those coordinates in the two functions verifies that those are the other two corners.
However, it is useful to go through the formal algebra to show that the points of intersection of the two graphs are (-1,3) and (3,1).
We need to solve

The behavior of the two functions change at x=0 and x=2, so we need to check for solutions on three intervals: (1) x less than 0, (2) x between 0 and 2, and (3) x greater than 2.
(1) for x negative,  and and 
2-x=4+x
2x=-2
x=-1 --> y=3
(2) for x between 0 and 2,  and and 
2-x = 4-x
2=4
there is clearly no intersection of the two graphs between x=0 and x=2.
(3) for x greater than 2,  and and 
x-2=4-x
2x=6
x=3 --> y=1
So indeed the four corners of the rectangle are (2,0), (-1,3), (0,4), and (3,1).
The width of the rectangle is the distance between (2,0) and (3,1), which is  . .
The length of the rectangle is the distance between (2,0) and (-1,3), which is  . .
The area of the rectangle is then length times width: 
|
|
|