|
Question 1191567: In the planning of a coffee shop, the daily profit is estimated to be $16 per place if there are places for 40 to 80 people. However, if the seating capacity is more than 80 places, the daily profit on each place will be decreased by $0.08 times the number of places above 80. What should be the seating capacity to yield the greatest daily profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it looks to me like you have two equations.
one equation is for 40 <= x <= 80
the other equation for x > 80.
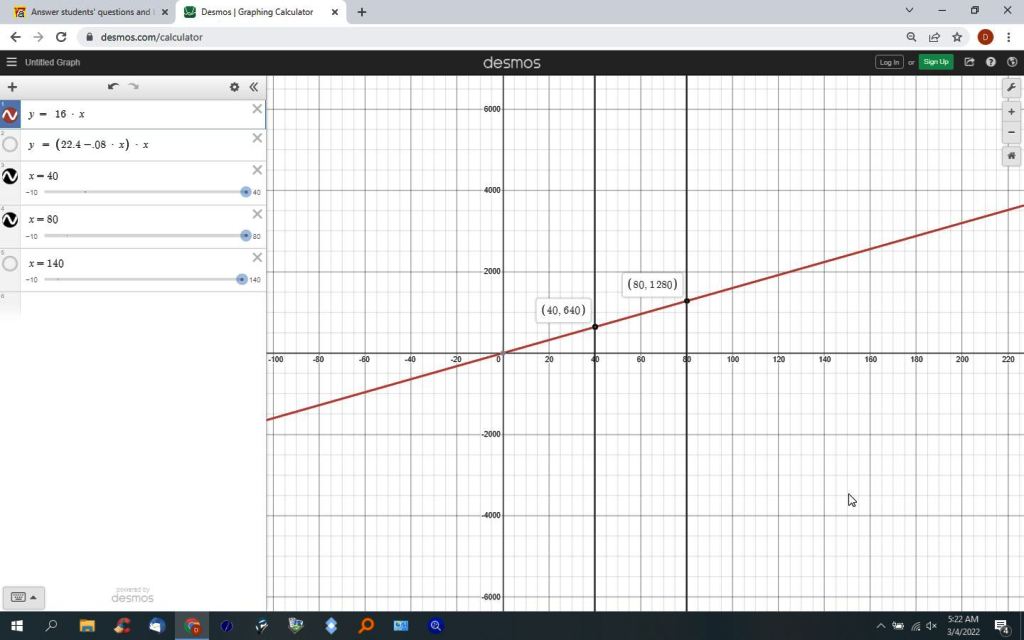
for x = 40 to 80, the equation is y = 16 * x.
it's a straight line equation and it will max out at x = 80.
for x > 80, the equation is y = (16 - .08 * (x - 80)) * (80 + (x - 80)).
this equation can be simplified to y = (16 - .08 * x + .08 * 80) * x.
simplify further to get y = (22.4 - .08 * x) * x.
simplify further to get y = 22.4 * x - .08 * x^2.
you have two equations.
y = 16 * x for 40 <= x <= 80
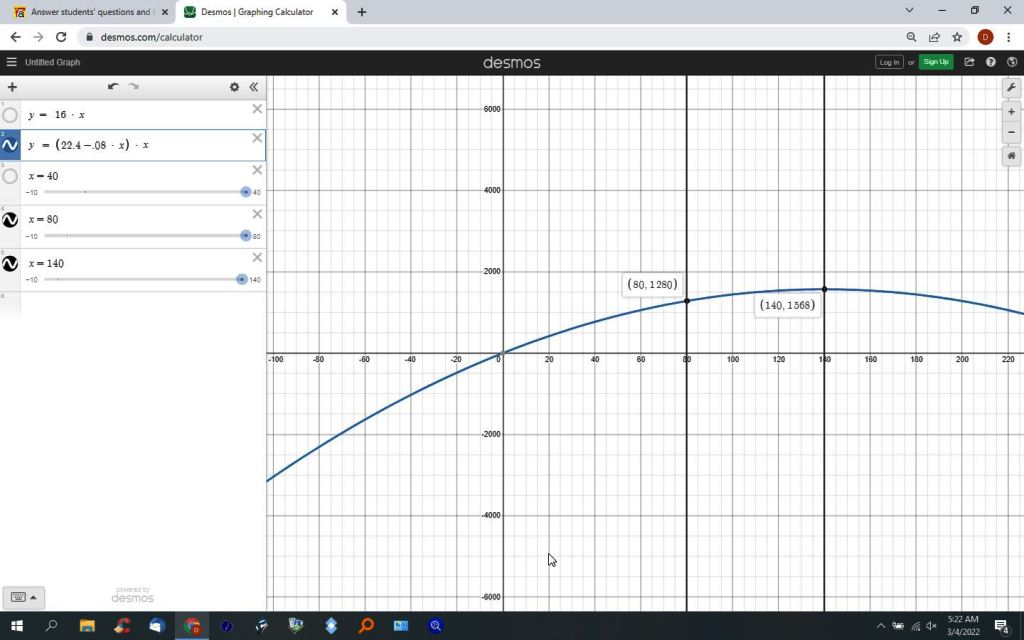
y = 22.4 * x - .08 * x^2 for x >= 80
when x = 80, the first equation gives you 16 * 80 = 1280 and the second equation gives you 22.4 * 80 - .08 * 80^2 = 1280.
in other words, they give you the same daily profit when x = 80.
you use the first equation for 40 <= x <= 80
you use the second equation for x > 80.
when x = 81, the daily profit will be 22.4 * 81 - .08 * 81^2 = 1289.52.
this is the same as (16 - .08 * 1) * (80 + 1) = 1289.52.
when x = 82, the daily profit will be 22.4 * 82 - .08 * 82^2 = 1298.88.
this is the same as (16 - .08 * 2) * (80 + 2) = 1298.88
the daily profit will keep rising until you hit 140 places.
when x = 140, 22.4 * 140 - .08 * 140^2 = 1568.
this is the same as (16 - .08 * 60) * (80 + 60) = 1568.
after 140 places, the daily profit starts declining.
at 141 places, the daily profit will be 22.4 * 141 - .08 * 141^2 = 1567.2.
it keeps going down from there.
i graphed the two equations.
the graphs looks like this.
the first graph is for 40 <= x <= 80
the second graph is for x >= 80
the third graph combine them into one graph.
the red equation is for 40 <= x <= 80
the blue equation is for x >= 80
both equations give you the same value at x = 80.
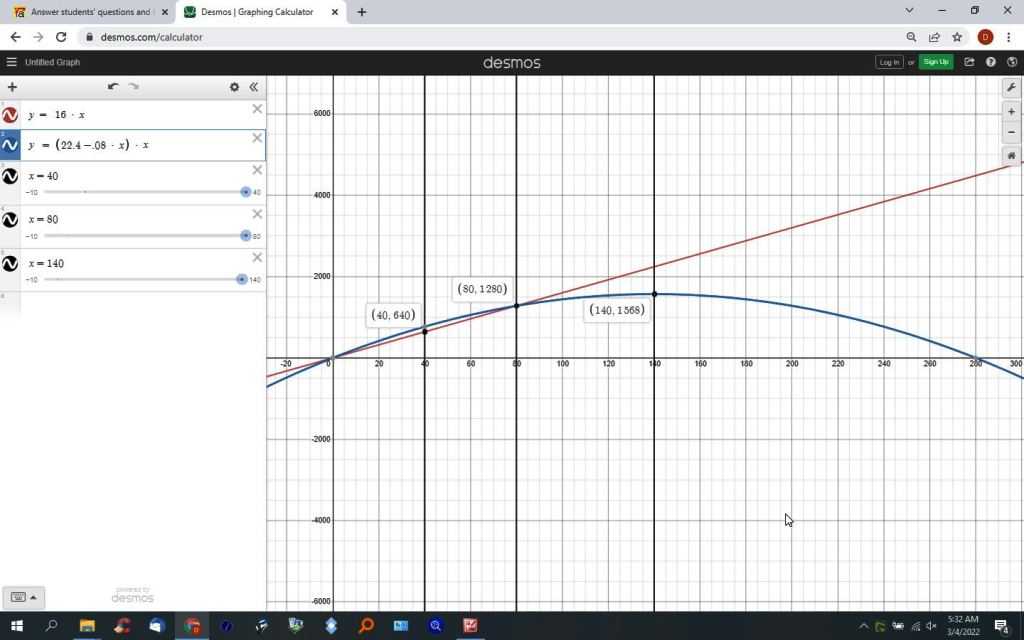
assuming i did this correctly, the maximum daily profit will be when 140 places are available and used.
the quadratic equation is y = 22.4 * x - .08 * x^2
reorder the terms in descending order of degree and you get y = -.08 * x^2 + 22.4 * x.
since this equation is in standard form, then:
a = 22.4 and b = -.08.
the maximum value will be when x = -b/(2a) which becomes x = -22.4 / -.16 = 140, as shown on the graph.
|
|
|
| |