Question 1191331: According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. You randomly select peanut M&M’s from an extra-large bag looking for a yellow candy. (Round all probabilities below to four decimal places; i.e. your answer should look like 0.1234, not 12.34%.)
a) Compute the probability that the first yellow candy is the sixth M&M selected.
b) Compute the probability that the first yellow candy is the sixth or seventh M&M selected.
c) Compute the probability that the first yellow candy is among the first six M&M’s selected.
d) If every student in a large Statistics class selects peanut M&M’s at random until they get a yellow candy, on average how many M&M’s will the students need to select? (Round your answer to two decimal places.)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow,
12% are red, 23% are blue, 23% are orange and 15% are green.
You randomly select peanut M&M’s from an extra-large bag looking for a yellow candy.
(Round all probabilities below to four decimal places; i.e. your answer should look like 0.1234, not 12.34%.)
a) Compute the probability that the first yellow candy is the sixth M&M selected.
b) Compute the probability that the first yellow candy is the sixth or seventh M&M selected.
c) Compute the probability that the first yellow candy is among the first six M&M’s selected.
d) If every student in a large Statistics class selects peanut M&M’s at random until they get a yellow candy,
on average how many M&M’s will the students need to select? (Round your answer to two decimal places.)
~~~~~~~~~~~~~~~~
Tooooooo many questions to answer all of them at a time.
In this post, I will answer (a), (b) and (c), only.
The major idea is to recognize that we have a Binomial distribution probability problem with the success
individual trial probability of 0.15 for yellow and (1-0.15) = 0.85 for not yellow.
(a) P(the first yellow candy is the sixth M&M selected) = 0.85^5*0.15 = 0.06656 (rounded).
(b) P(the first yellow candy is the sixth or seventh M&M selected) = 0.85^5*0.15 + 0.85^6*0.15 = 0.1231 (rounded).
(c) P(the first yellow candy is among the first six M&M’s selected) =
= is the same as (simply re-phrasing) =
= P(exactly one yellow is among the first six M&M’s selected) =
=  = = 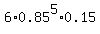 = 0.3993. = 0.3993.
|
|
|