SOLUTION: How many different permutations can be formed from the letters in the word "essence"

Algebra ->  Probability-and-statistics -> SOLUTION: How many different permutations can be formed from the letters in the word "essence"      Log On


   

Question 1191201: How many different permutations can be formed from the letters in the word "essence"
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
How many different permutations can be formed from the letters in the word "essence"
~~~~~~~~~~~~~~~~~ 

The word has 7 letters; of them,  " e "  has the multiplicity 3 and  " s "  has multiplicity 2.


Therefore, the formula for the number of distinguishable permutations / (arrangements) is


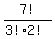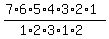    7%21%2F%283%21%2A2%21%29 = %287%2A6%2A5%2A4%2A3%2A2%2A1%29%2F%281%2A2%2A3%2A1%2A2%29 = 420.    ANSWER

Solved.

-----------------

To see many other similar  (and different)  solved problems,  look into the lesson
    - Arranging elements of sets containing indistinguishable elements
in this site.