SOLUTION: x + y + z =6 x+2y+3z=10 x+2y+az=b)

Algebra ->  Expressions-with-variables -> SOLUTION: x + y + z =6 x+2y+3z=10 x+2y+az=b)      Log On


   

Question 1191180: x + y + z =6
x+2y+3z=10
x+2y+az=b)
Found 3 solutions by MathLover1, Edwin McCravy, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

x+%2B+y+%2B+z+=6........1)
x%2B2y%2B3z=10.......2)
x%2B2y%2Baz=b.........3)
___________________________


x+%2B+y+%2B+z+=6........1)
x%2B2y%2B3z=10.......2)
____________________________subtract
x%2B2y%2B3z-x+-+y+-+z+=10-6
y%2B2z++=4.......solve for y
y++=4-2z............1.1)

x+%2B+y+%2B+z+=6........1).........substitute y
x+%2B+4-2z+%2B+z+=6.....solve for x
x+%2B+4-z++=6
x+=z-4%2B6
x+=z%2B2...............1.2)


x%2B2y%2Baz=b.........3)........substitute x, y,
z%2B2%2B2%284-2z%29%2Baz=b.....solve for z
z%2B2%2B8-4z%2Baz=b
z%2B10-4z%2Baz=b
az-3z=b-10
%28a-3%29z=b-10
z=%28b-10%29%2F%28a-3%29...........1.3)


then
x+=%28b-10%29%2F%28a-3%29%2B2...............1.2)
and
y++=4-2%28%28b-10%29%2F%28a-3%29%29............1.1)


The solutions to the system of equations are:

x=%28b-10%29%2F%28a-3%29%2B2
y=4-%282%28b-10%29%2F%28a-3%29%29+
z=%28b-10%29%2F%28a-3%29 where+a%3C%3E3


Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!


Case 1: a=3.





-1R1+R2->R2



-1R2+R1->R1



system%281x%2B0y-1z=2%2C0x%2B1y%2B2z=4%2C0x%2B0y%2B0z=0%29

system%28x-z=2%2Cy%2B2z=4%29

system%28x=2%2Bz%2Cy=4-2z%29

(x,y,z) = (2+z,4-2z,z) where z is arbitrary.

Some solutions from case 1 are (x,y,z)=(2,4,0), (x,y,z)=(3,2,1),
(x,y,z)=(4,0,2), (x,y,z)=(5,-2,3), (x,y,z)=(1,6,-1), etc., etc.,...

Case 2. x ≠ 3    



-1R2+R1->R1



-1R1+R2->R2



-1R1+R3->R3



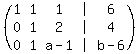-1R2+R1->R1



-1R2+R3->R1



-1R2+R3->R3



1/(a-3)*R3->R3



R3+R1->R1



-2R3+R2->R2



Simplifying:





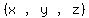%28matrix%281%2C5%2Cx%2C%22%2C%22%2Cy%2C%22%2C%22%2Cz%29%29%22%22=%22%22

Edwin

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

            This post came with no question, which makes me very sad
            (as usual as I see such an inaccuracy and disrespect to the tutors).

            The short resume to this problem is as follows. 


(1)  The case a= 3 is special.


     If  a= 3 and b= 10, then there are infinitely many solutions.

                         In this case, the system is dependent.


     If a= 3 and b =/= 10, then there is NO solutions and the system is inconsistent.



(2)  If a =/= 3, then we have three independent equations;

                 the system is consistent and has a unique solution.

Answered.