Question 1191102: Generate truth table for the following functions.
A. F(X,Y,Z) =∑ ( 1,3,6, 7)
B. F(X,Y,Z) = π ( 1,3,4)
C. F( W, X,Y,Z) =∑ ( 1, 4, 7, 10, 12, 15)
D. F( W, X,Y,Z) =π( 2,3, 4, 7, 10, 11, 12, 13)
Could you explain me this homework question step-by-step please? Thank you very much!!!
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll do the first two parts (A and B) to get you started.
===========================================================================================
Part A
At this point in your Boolean Algebra class, you should be pretty familiar with binary numbers (and how to count in binary).
If not, then please revise those rules before reading on.
Start at 000 and count upward in binary until you reach 111.
000
001
010
011
100
101
110
111
As you can see, we have accounted for all possible combos of 1's and 0's when considering three slots.
A few patterns to point out:- The first column has four "0"s in a row, followed by four "1"s in a row.
- The second column has two identical copies of "0011".
- The third column has four copies of "01" repeated.
The first binary digit accounts for X
If the first digit is 1, then we go for X
If the first digit is 0, then we go for the complement X'
The same goes for the second and third digits (but we use Y and Z for them).
A string like 000 means we have X'Y'Z'
001 means X'Y'Z
010 means X'YZ'
and so on
Here's a table of the minterms m0 through m7 (for 3 variables).
| Minterms | | X | Y | Z | Term | Designation | | 0 | 0 | 0 | X'Y'Z' | m0 | | 0 | 0 | 1 | X'Y'Z | m1 | | 0 | 1 | 0 | X'YZ' | m2 | | 0 | 1 | 1 | X'YZ | m3 | | 1 | 0 | 0 | XY'Z' | m4 | | 1 | 0 | 1 | XY'Z | m5 | | 1 | 1 | 0 | XYZ' | m6 | | 1 | 1 | 1 | XYZ | m7 |
Minterms are products of literals.
A literal is simply an atomic variable such as X, Y or Z. It also involves the complements of such (eg: X')
"product" refers to the "AND" boolean operation.
Instead of writing X'Y'Z', we can use the shorthand designation of m0. This m is lowercase.
I could write m0 as 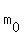 but I'll stick to the first notation format. but I'll stick to the first notation format.
-----------------
So with all this in mind, we can now finally address the notation ∑ ( 1,3,6, 7)
The sigma indicates we'll be adding the minterms m1, m3, m6, and m7
Though of course the addition symbol means we use the boolean "OR" operator.
So,
∑ ( 1,3,6, 7) = m1 + m3 + m6 + m7
Use that table formed earlier to replace each of those m values
∑ ( 1,3,6, 7) = m1 + m3 + m6 + m7
∑ ( 1,3,6, 7) = X'Y'Z + X'YZ + XYZ' + XYZ
If you don't have the table handy, then you can either recreate it or you can take note that something like the "3" from "m3" corresponds to the binary 011. This means we'll have X', Y and Z all multiplied together. Well by "multiply", I of course mean the boolean "AND" operation.
I like to think of it as a set of light switches to flip on or off
011 = off,on,on = X'YZ
Let's generate the truth table based on this.
I strongly recommend using spreadsheet software to quickly calculate each cell value.
Though you could do it by hand if you prefer.
When using the spreadsheet program, be sure to make use of the functions labeled "AND", "OR", "NOT"
To convert from "TRUE"/"FALSE" to their numeric counterpart, multiply the result by 1.
Review the spreadsheet help manual and/or question forums if you get stuck anywhere.
Also, feel free to ask me about any particular spreadsheet function.
Here is one example of what a particular cell could look like using the functions mentioned =AND(E9,F9,D9)*1
Don't forget about the equal sign up front or else the function won't evaluate. Instead, it'll be rendered as text only.
Check out the spreadsheet I made here to see the truth table.
https://docs.google.com/spreadsheets/d/1-T6KukyyuJujfWou7l6IZnZ8zNU9yKlJQOrAtr4EC7s/edit?usp=sharing
You do not need a google account to be able to view the page.
===========================================================================================
Part B
The π symbol means "product" or "multiply". Normally it's written in a big font and uppercase like this  to avoid confusion with the famous constant pi = 3.14... to avoid confusion with the famous constant pi = 3.14...
The π for this boolean algebra course means we will involve the "AND" operator.
Before we can jump into translating that notation, we first need to set up the standard table.
It's very similar to the previous table with two key differences
The first key difference is that we replace every multiplication symbol with a plus sign.
The second key difference is that we flip each X to X', and vice versa. Same goes for Y to Y' and Z to Z'.
For example, the minterm m0 = X'Y'Z' will correspond to the maxterm M0 = X+Y+Z
Another example: the minterm m6 = XYZ' corresponds to the maxterm M6 = X'+Y'+Z
As you can see, a maxterm is a sum of literals while a minterm is a product of literals.
By convention, minterms use lowercase m's while maxterms use uppercase M's.
It's probably a bit weirdly confusing why we flip terms like this.
But consider De Morgan's Law which says
(X+Y)' = X'Y'
and
(XY)' = X'+Y'
The 3 variable version of De Morgan's Law is
(X+Y+Z)' = X'Y'Z'
and
(XYZ)' = X'+Y'+Z'
That's effectively what's going on when swapping between minterms and maxterms.
This is a useful maxterms table (3 variables)
| Maxterms | | X | Y | Z | Term | Designation | | 0 | 0 | 0 | X+Y+Z | M0 | | 0 | 0 | 1 | X+Y+Z' | M1 | | 0 | 1 | 0 | X+Y'+Z | M2 | | 0 | 1 | 1 | X+Y'+Z' | M3 | | 1 | 0 | 0 | X'+Y+Z | M4 | | 1 | 0 | 1 | X'+Y+Z' | M5 | | 1 | 1 | 0 | X'+Y'+Z | M6 | | 1 | 1 | 1 | X'+Y'+Z' | M7 |
Now to address the notation π(1,3,4)
It refers to multiplying the maxterms of: M1, M3, M4
The table above says:
M1 = X + Y + Z'
M3 = X + Y' + Z'
M4 = X' + Y + Z
So,
π(1,3,4) = M1 * M3 * M4
π(1,3,4) = ( M1 ) * ( M3 ) * ( M4 )
π(1,3,4) = (X + Y + Z') * (X + Y' + Z') * (X' + Y + Z)
The truth table of this is in the part B section of the google spreadsheet link above.
===========================================================================================
Parts C and D will follow similar steps as parts A and B respectively.
Though of course now we have 4 literals for each, meaning that the standard tables will need to be updated to reflect this. You'll have to count upward in binary from 0000 to 1111 to get the 16 minterms and 16 maxterms needed.
You probably have such similar tables in your textbook or on some reference sheet elsewhere (or perhaps your teacher has a handy reference you can use). So you won't always need to generate those standard tables.
Side notes:
It's probably tempting to put a space between "min" and "term" when writing out "minterm", but it's actually one word instead of two. The same goes for "maxterm".
Another term for "minterm" is "standard product".
Another term for "maxterm" is "standard sum".
|
|
|