|
Question 1190912: Explain the transformations you would need to apply to the graph of y=f(x) to graph the function
y=-f(1/4x+6) -7
Answer by greenestamps(13215)   (Show Source):
You can put this solution on YOUR website!
For clarity, rewrite the new function as
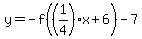
Then rewrite the new function in the form
The transformations will be, in order,
(1) translation of c units
(2) horizontal compression by a factor of b
(3) vertical stretch by a factor of a
(4) vertical translation by d
Note the "(1/4)x+6" needs to be rewritten as "(1/4)(x+24)".
The rest is straightforward....
--> 
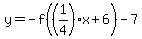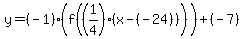
That gives us a=-1, b=1/4, c=-24, and d=-7
The transformations are then, in order,
(1) translation 24 units left
(2) horizontal compression by a factor of 1/4
(3) vertical stretch by a factor of -1 (i.e., reflect over the x-axis)
(4) vertical translation down 7
-----------------------------------------------------------------------
In reply to the student's comment....
A horizontal compression by a factor of a is a horizontal stretch by a factor of 1/a. So in this example, the compression by a factor of 1/4 is a stretch by a factor of 4.
That is the correct interpretation.
As an example, consider f(x)=sin((1/4)x). The compression factor is 1/4 which means there is a horizontal stretch by a factor of 4.
This is correct, because the function sin((1/4)x) completes a cycle every 8pi ( -->  ), while the function sin(x) completes a cycle every 2pi -- the graph is stretched horizontally by a factor of 4.
|
|
|
| |
