Question 1190899: I need your help with this!
Assume Pr[A]=0.3, Pr[B]=0.4, and Pr[A∩B]=0.05. Find the following values:
Pr[B|A] =
Pr[A|B′] =
Pr[B′|A′] =
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I need your help with this!
Assume Pr[A]=0.3, Pr[B]=0.4, and Pr[A∩B]=0.05. Find the following values:
(a) Pr[B|A] =
(b) Pr[A|B′] =
(c) Pr[B′|A′] =
~~~~~~~~~~~~~~~~~~~~
In this problem, all questions ask about CONDITIONAL PROBABILITY.
To solve the problem and to answer all the questions, you need firmly know WHAT the conditional probability is.
If X and Y are the events in the universal set of events, then P(X|Y) is THIS ratio
P(X|Y) = 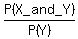 . .
Having this definition, let answer all questions, one after other.
(a) P(B|A) =  = = 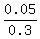 = =  = =  . ANSWER
Solved. So, it is easy.
(b) P(A|B').
We should find P(A ∩ B'). The set (A ∩ B') are those elements/(events) of A that do not belong to B.
From it, it is clear that the set (A ∩ B') is (A \ (A ∩ B)).
Therefore, P(A ∩ B') = P(A) - P(A ∩ B) = 0.3 - 0.05 = 0.25.
Next, P(B') = 1 - P(B) = 1 - 0.4 = 0.6.
THEREFORE, P(A|B') = . ANSWER
Solved. So, it is easy.
(b) P(A|B').
We should find P(A ∩ B'). The set (A ∩ B') are those elements/(events) of A that do not belong to B.
From it, it is clear that the set (A ∩ B') is (A \ (A ∩ B)).
Therefore, P(A ∩ B') = P(A) - P(A ∩ B) = 0.3 - 0.05 = 0.25.
Next, P(B') = 1 - P(B) = 1 - 0.4 = 0.6.
THEREFORE, P(A|B') =  = = 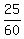 = = 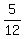 . ANSWER
(c) P(A'|B').
We should find P(A' ∩ B'). The set (A' ∩ B') are those elements/(events) of the universal set that belong NEITHER A NOR B.
From it, it is clear that the set (A' ∩ B') is the complement of (A U B).
P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.3 + 0.4 - 0.05 = 0.65.
Therefore, P(A' ∩ B') = 1 - P(A U B) = 1 - 0.65 = 0.35.
Next, P(B') = 1 - P(B) = 1 - 0.4 = 0.6.
THEREFORE, P(A'|B') = . ANSWER
(c) P(A'|B').
We should find P(A' ∩ B'). The set (A' ∩ B') are those elements/(events) of the universal set that belong NEITHER A NOR B.
From it, it is clear that the set (A' ∩ B') is the complement of (A U B).
P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.3 + 0.4 - 0.05 = 0.65.
Therefore, P(A' ∩ B') = 1 - P(A U B) = 1 - 0.65 = 0.35.
Next, P(B') = 1 - P(B) = 1 - 0.4 = 0.6.
THEREFORE, P(A'|B') = 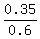 = =  = =  . ANSWER . ANSWER
------------
Solved.
All questions are answered.
|
|
|