Question 1190890: Find the coordinates of the foci, the endpoints of the major axis, minor axis and the latus rectum.
x^2/169+y^2/144=1
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
 -> this is an ellipse -> this is an ellipse
compare to standard form  and you see that and you see that
 and and 
 -> ->
 -> ->



the coordinates of the foci: (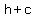 , , ) and ( ) and (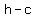 , , ) )
since  and and  , foci are at ( , foci are at ( , , ) and ( ) and ( , , ) )
so, foci are at: ( , ,  ) and ( ) and ( , ,  ) )
the major axis: 
minor axis: 
the endpoints of the major axis are at vertices : ( , , ) and ( ) and ( , , ) )
( , , ) and ( ) and ( , , ) )
the endpoints of the minor axis are at co-vertices : ( , , ) and ( ) and ( , , ) )
( , , ) and ( ) and ( , , ) )
the latus rectum:
latus rectum of an ellipse is nothing but 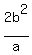


|
|
|