SOLUTION: An airplane is flying at a speed of 250 mph at an altitude of 5 miles. The plane passes directly above a radar station at time t = 0. Find the distance s between the plane and the

This distance is the hypotenuse of the right-angled triangle, one leg of which

is the altitude (5 miles), and the other leg is the horizontal travel distance

of the plane in 5 minutes.


This horizontal distance is 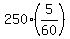  miles = 20.833 miles.


So, the distance from the radar to the plane is  


      d = 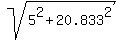 = 21.425 miles.    ANSWER