SOLUTION: Given that f (x)= 3x+4/2x-3 is a one-to-one function, (a) find f^-1(-1) (b) show f^-1 (f(x))=x

(a)  To find  f^-1(-1),  you do not need express  f^-1(x) in explicit form : it is UNNECESSARY job.


     What you really need, is to solve equation  f(x) = -1  and find x  in this way;  

     then the found value of x will be your answer, i.e. f^-1(-1).


     So, I will do it:  I will solve equation


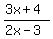          = -1.


      To solve, multiply both sides by  (2x-3);  then simplify


          3x + 4 = -(2x-3)

          3x + 4 = -2x + 3

          3x + 2x = 3 - 4

             5x   =   -1

              x   =  = -0.2.      ANSWER




(b)  Since it is given in the post that the function f(x) is one-to-one,

     the inverse function  f^-1(x) does exist.


     For me, it does not matter now what is its concrete expression.


     But for the inverse function,  the requested identity


         f^-1 (f(x))=x


     is valid by the DEFINITION:  so,  THERE IS NOTHING TO PROVE  in this case.



     Notice and understand, that my reasoning is absolutely correct in this case: 

         there is NOTHING TO PROVE: the statement follows immediately from the definition and from the given part.