Question 1190671: MAT 145: Topics In Contemporary Math
Sets and Set Operations
Given the definitions for the sets, find the elements in the subsets in roster notation.
Universal set U = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}
A = {5, 15, 25, 35, 45}
B = {10, 15, 25, 35}
𝐴 ∪ 𝐵 𝐴 ∩ 𝐵 𝐴^c
𝐵^c (𝐴 ∪ 𝐵)^c
Found 2 solutions by Alan3354, Stelless:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by Stelless(3)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm unsure about the format of your questions but I will try my best with what is provided.
Given the definitions for the sets, find the elements in the subsets in roster notation.
Universal set = U
U = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}
A = {5, 15, 25, 35, 45}
B = {10, 15, 25, 35}
1) 𝐴 ∪ 𝐵
2) 𝐴 ∩ 𝐵
3) A^c
4) 𝐵^c
5) (𝐴 ∪ 𝐵)^c
Note: Roster Notation just means listing the elements in curly brackets (note that all of these sets A, B, U are given in roster notation).
1) (A U B). The '∪' in this statement is called Union. Sometimes we refer this as an 'or' statement. Read allowed we can read this as "A or B" which means that it includes the values the sets together. So we simply stitch the sets together.
- A = {5, 15, 25, 35, 45}
- B = {10, 15, 25, 35}
- (A ∪ B) = {5, 10, 15, 15, 25, 25, 35, 35, 45}
Sets do not contain repeated elements though so we simply remove duplicates:
- (A ∪ B) = {5, 10, 15, 25, 35, 45}
2) (A ∩ B). The "∩" symbol is called intersection. This means the value of this set ( A ∩ B) will be where the two sets intersect (or where they share elements).
- A = {5, 15, 25, 35, 45}
- B = {10, 15, 25, 35}
notice the values "15, 25, 35" are in both sets. These values represent where they intersect.
- (A ∩ B) = { 15, 25, 35}
3) 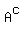
This "^c" symbol means the 'compliment' or 'not A'. These are just all the elements that exist (in our universal set) but are not in A already.
U = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}
A = {5, 15, 25, 35, 45}
A^c = {10, 20, 30, 40, 50}
4) 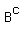
These are all the elements that exist but that are not in B already.:
U = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}
B = {10, 15, 25, 35}
B^C = {5, 20, 30, 40, 45, 50}
5) (𝐴 ∪ 𝐵)^c
This is a compound statement with two things happening:
First, we are taking the union of A & B. We've already done this and Part 1:
- (A ∪ B) = {5, 10, 15, 25, 35, 45}
Then we are asked to take the compliment of this set. So we simply add the elements that exist but aren't in (A U B) already.
U = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}
(A ∪ B) = {5, 10, 15, 25, 35, 45}
(𝐴 ∪ 𝐵)^c = {20, 30, 40, 50}
|
|
|