Question 1190367: Having trouble figuring out how to factor this problem.
Factor completely given that x-3 is a factor of x^3-5x^2-14x+60.
I tried grouping to factor and it isn't working.
Found 6 solutions by MathLover1, greenestamps, MathTherapy, math_tutor2020, ikleyn, josgarithmetic:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(original response deleted)
I used the polynomial shown by the first tutor, which was not the given polynomial...
Use synthetic division as shown by tutor @math_tutor2020 to complete the factoring.
And by the way, factoring a polynomial with four terms by grouping only works in very special cases, like this:

Note the coefficient of the x term (-4) is -4 times the coefficient of the x^3 term (1), and the constant term (12) is -4 times the coefficient of the x^2 term (-3). Since both those ratios are the same, the polynomial can be factored by grouping.

Since the coefficients in the given polynomial do not have a pattern like that, the polynomial can't be factored by grouping.
--------------------------------------------------------------------
A further note, in response to the statement from tutor @ikleyn that my statement that this polynomial can't be factored by grouping is incorrect.
In fact my statement is correct: this polynomial can't be factored by grouping.
Factoring by grouping consists of grouping the four terms into two groups of two terms each and factoring the common factor out of each pair to obtain a factorization.
The process she uses of "grouping/regrouping" can be used to factor ANY polynomial given one of the binomial factors... but that process is NOT factoring by grouping.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Having trouble figuring out how to factor this problem.
Factor completely given that x-3 is a factor of x^3-5x^2-14x+60.
I tried grouping to factor and it isn't working.
Those 2 people are WRONG!
One claims that x - 3 is not a factor. That's a FALDEHOOD! The other claims that the divisor x - 3 yields a
remainder of - 54. Total FALSEHOOD also. 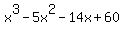 factors to factors to 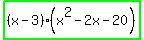
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Remainder Theorem:
If p(x) is divided over (x-k), then p(k) is the remainder.
Comparing x-3 to x-k shows that k = 3
p(x) = x^3-5x^2-14x+60
p(3) = 3^3-5(3)^2-14(3)+60
p(3) = 0
A remainder of zero confirms that x-3 is indeed a factor of x^3-5x^2-14x+60
Here's the polynomial long division

And here's what the synthetic division looks like

Either way, you should find that
x^3-5x^2-14x+60 = (x-3)(x^2-2x-20)
You can use WolframAlpha or GeoGebra's CAS calculator to confirm. There are numerous other free calculators that will do the same type of thing.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Having trouble figuring out how to factor this problem.
Factor completely given that x-3 is a factor of x^3-5x^2-14x+60.
I tried grouping to factor and it isn't working.
~~~~~~~~~~~~~~~~
Having given that (x-3) is a factor of x^3 - 5x^2 - 14x + 60 is a very
significant piece of information. Having it, you can divide the given polynomial
by linear factor (x-3) without a remainder and get the quotient, which is
a quadratic polynomial. It is the standard way to proceed in this case.
+----------------------------------------------------------------------------+
| But grouping-regrouping ALSO WORKS in this case, despite the statement |
| |
| made by @greenestamps. I will show you below HOW IT WORKS. |
+----------------------------------------------------------------------------+
So, I start with this polynomial (x^3 - 5x^2 - 14x + 60).
Since I am given that (x-3) is the factor, I will extract the leading part of the polynomial
in the form (x^3 - 3x^2), leaving the rest for the other part
x^3 - 5x^2 - 14x + 60 = (x^3 - 3x^2) + (-2x^2 - 14x + 60) = x^2*(x-3) + (-2x^2 - 14x + 60). (1)
Further, I will work with this remaining part, keeping the leading part of the polynomial as is. So
x^2*(x-3) + (-2x^2 - 14x + 60) = x^2*(x-3) - 2*(x^2 + 7x - 30). (2)
Next, I can easily factor the last trinomial, and the fact that (x-3) is the factor, WILL HELP ME AGAIN
x^2*(x-3) - 2*(x^2 + 7x - 30) = x^2*(x-3) - 2*(x-3)*(x+10) = (x-3)*(x^2 - 2(x+10)) = (x-3)*(x^2 - 2x - 20). (3)
Combining lines (1), (2) and (3), I get the final decomposition
x^3 - 5x^2 - 14x + 60 = (x-3)*(x^2 - 2x - 20).
So, I did it using grouping-regrouping.
Surely, direct division (long division or synthetic division) is more straightforward way,
but grouping-regrouping DOES WORK, TOO, and the given info about a / (the) linear factor helps you to do it
from the beginning to the end, through all intermediate steps.
Solved by grouping-regrouping, for your better understanding.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
|
|
|