Question 1190364: Carbon-14 is used to determine the age of artifacts. It has a half-life of 5700 years. This means that
in 0 years 100%, of the original amount of carbon-14 remains in the artifact. In 5700 years 50% of
the original amount of carbon-14 remains.
a) Suppose that 40% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
b) Suppose that 75% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
c) Suppose that 2% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the half life formula is:
.5 = (1 + r) ^ 5700
1 + r is the growth factor per year.
take the 5700th root of both sides of this equation to get:
.5 ^ (1/5700) = 1 + r
solve for 1 + r to get:
1 + r = .9998784026.
that number is rounded to the number of decimal digits displayed in the calculator.
to get the most accurate value when using that factor, use the internally stored value rather than the displayed value.
to confirm the value is correct, then:
1 * .9998784026 ^ 5700 = .4999999286, using the displayed value.
1 * .999878402... ^ 5700 = .5, using the stored value in the calculator,.
now that you know the rate per year, you can solve for the rest of the problem.
a) Suppose that 40% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
b) Suppose that 75% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
c) Suppose that 2% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
start with .5 = x ^ y
x is equal to our stored value of .9998784026.
note that this is the displayed value of x.
the actual value of x is stored in the calculator and has more decimal digits than the displayed value.
we want to solve for y.
take the log of both sides of this equation to get:
log(.5) = y * log(x).
divide both sides of this equaiton by log(x) to get:
log(.5) / log(x) = y
solve for y to get:
y = 5700.
note that, since x = .9998784026, the equation is really:
log(.5) / log(.998784026) = y.
once again, you are using the stored value of x and not the displayed value of x, for greater accuracy.
this confirms that we can find the value of y using this formula.
the value of y is the number of years.
now to solve the rest of the problems.
a) Suppose that 40% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
if 40% of the original carbon remains, then the formula becomes:
log(.4) / log(x) = y
solve for y to get:
y = 7534.990141.
b) Suppose that 75% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
if 75% of the original carbon remains, then the formula becomes:
log(.75) / log(x) = y
solve for y to get:
y = 2365.713746.
c) Suppose that 2% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
if 2% of the original carbon remains, then the formula becomes:
log(.02) / log(x) = y
solve for y to get:
y = 32169.98028
the equation can be graphed as shown below:

let me know if you have any questions.
theo
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Carbon-14 is used to determine the age of artifacts. It has a half-life of 5700 years. This means that
in 0 years 100%, of the original amount of carbon-14 remains in the artifact. In 5700 years 50% of
the original amount of carbon-14 remains.
a) Suppose that 40% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
b) Suppose that 75% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
c) Suppose that 2% of the original carbon remains in a piece of pottery.
Estimate the age of the pottery.
~~~~~~~~~~~~~~
You are given that half-life of C-14 is 5700 years.
So, you can write the decay function in the form
m(t) = 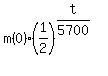 , (1)
where m(0) is the original mass, m(t) is the current mass and t is the time, in years.
To answer all questions that follow, divide both sides of the decay equation (1) by m(0). You will get , (1)
where m(0) is the original mass, m(t) is the current mass and t is the time, in years.
To answer all questions that follow, divide both sides of the decay equation (1) by m(0). You will get
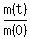 = =  . (2)
Now let's answer the questions, one after another.
(a) You are given . (2)
Now let's answer the questions, one after another.
(a) You are given 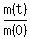 = 40% = 0.4.
So, equation (2) gives you = 40% = 0.4.
So, equation (2) gives you
 = 0.4.
Take logarithm base 10 of both sides = 0.4.
Take logarithm base 10 of both sides
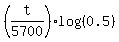 = log(0.4)
t = = log(0.4)
t =  = 7535 years. ANSWER
(b) You are given = 7535 years. ANSWER
(b) You are given 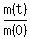 = 75% = 0.75.
So, equation (2) gives you = 75% = 0.75.
So, equation (2) gives you
 = 0.75.
Take logarithm base 10 of both sides = 0.75.
Take logarithm base 10 of both sides
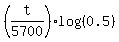 = log(0.75)
t = = log(0.75)
t =  = 2366 years. ANSWER
(c) You are given = 2366 years. ANSWER
(c) You are given 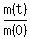 = 2% = 0.02.
So, equation (2) gives you = 2% = 0.02.
So, equation (2) gives you
 = 0.02.
Take logarithm base 10 of both sides = 0.02.
Take logarithm base 10 of both sides
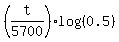 = log(0.02)
t = = log(0.02)
t = 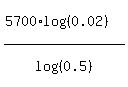 = 32170 years. ANSWER = 32170 years. ANSWER
Solved.
------------------
To solve the problem, you do not need make tons of unnecessary calculations, that @Theo makes in his post.
When you know the half-life, the way which I show you is the standard, shortest and straightforward way to solve the problem.
///////////////
There is a group of lessons in this site, which covers many similar problems on Carbon dating
- Using logarithms to solve real world problems, and
- Radioactive decay problems
- Carbon dating problems
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|