|
Question 1190343: I am really having a hard time understanding solving using substitution
2x+3y=24
-3x-5y=15
how do I solve those using substitution
Found 3 solutions by Theo, MathLover1, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! with substitution, you solve for one of the variable in terms of the other variable in one of the equations and then you use that value to solve for the other variable in the other equation.
it's a way of reducing two unknown variable to one unknown variable.
a simpler example would be like this.
consider these two equations.
x + y = 1
2x + 3y = 10
solve for x in the first equation to get:
x = 1 - y
replace x in the second equation to get:
2 * (1 - y) + 3y = 10
simplify to get:
2 - 2y + 3y = 10
combine like terms to get:
2 + y = 10
solve for y to get:
y = 10 - 2 = 8.
now that you know the value of y, solve for x in either equation to get:
x + y = 1 becomes x + 8 = 1 which becomes x = -7.
your values are x = -7 and y = 8
go back to the original equations and replace a with -7 and y with 8.
you will get:
x + y = 1 becomes -7 + 8 = 1 which becomes 1 = 1 which is true.
2x + 3y = 10 becomes -14 + 24 = 10 which becomes 10 = 10 which is true.
this confirms the values of x and y are good because the same value of x and y make both equations true.
that was just an example.
your problem is a little more complicated because of the arithmetic involved but the concept is the same.
you are solving for one of the variables in terms of the other variable in one of the equation and you are using the result of that to solve for the other variable in the other equations.
your equations are:
2x + 3y = 24
-3x - 5y = 15.
take the first equation and solve for y in terms of x.
you will get x = (24 - 3y) / 2.
replace x with that in the second equation.
you will get:
-3x - 5y = 15 becomes:
-3 * [(24 - 3y) / 2] - 5y = 15
multiply both sides of that equation by 2 to get:
-3 * (24 - 3y) - 10y = 30
simplify to get:
-3 * 24 + 3 * 3y - 10y = 30
simplify further to get:
-72 + 9y - 10y = 30
combine like terms to get:
-72 - y = 30
add 72 to both sides of the equation to get:
-y = 102
solve for y to get:
y = -102
now that you know the value of y, you can use that value of y to solve for x in either of the original two equations.
2x + 3y = 24 becomes 2x + 3 * -102) = 24 which becomes 2x - 306 = 24 which becomes 2x = 330 which becomes x = 165.
-3x - 5y = 15 becomes -3x - 5 * -102 = 15 which becomes -3x + 510 = 15 which becomes -3x = -495.
solve for x to get:
x = -495 / -2 = 165.
your solution is that x = 165 and y = -102.
replace x and y with those values in the original equations and you will get:
2x+3y=24 becomes 2*165 - 3*102 = 24 which becomes 24 = 24 2 which is true.
-3x-5y=15 becomes -3*165 +5*102 = 15 which becomes 15 = 15 which is also true.
this confirm the solution is correct.
here's a reference on solving a system of equations simultaneously with substitution.
https://www.purplemath.com/modules/systlin4.htm
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 .....eq.1 .....eq.1
 ....eq.2 ....eq.2
_____________________________
| Solved by pluggable solver: Solving a linear system of equations by subsitution |
Lets start with the given system of linear equations


Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to choose y.
Solve for y for the first equation
 Subtract Subtract  from both sides from both sides
 Divide both sides by 3. Divide both sides by 3.
Which breaks down and reduces to
 Now we've fully isolated y Now we've fully isolated y
Since y equals 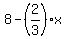 we can substitute the expression we can substitute the expression 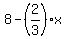 into y of the 2nd equation. This will eliminate y so we can solve for x. into y of the 2nd equation. This will eliminate y so we can solve for x.
 Replace y with Replace y with 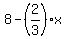 . Since this eliminates y, we can now solve for x. . Since this eliminates y, we can now solve for x.
 Distribute -5 to Distribute -5 to 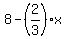
 Multiply Multiply
 Reduce any fractions Reduce any fractions
 Add Add  to both sides to both sides
 Combine the terms on the right side Combine the terms on the right side
 Make -3 into a fraction with a denominator of 3 Make -3 into a fraction with a denominator of 3
 Now combine the terms on the left side. Now combine the terms on the left side.
 Multiply both sides by Multiply both sides by 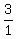 . This will cancel out . This will cancel out  and isolate x and isolate x
So when we multiply 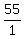 and and 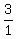 (and simplify) we get (and simplify) we get
 <---------------------------------One answer <---------------------------------One answer
Now that we know that  , lets substitute that in for x to solve for y , lets substitute that in for x to solve for y
 Plug in Plug in  into the 2nd equation into the 2nd equation
 Multiply Multiply
 Add Add 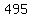 to both sides to both sides
 Combine the terms on the right side Combine the terms on the right side
 Multiply both sides by Multiply both sides by 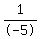 . This will cancel out -5 on the left side. . This will cancel out -5 on the left side.
 Multiply the terms on the right side Multiply the terms on the right side
 Reduce Reduce
So this is the other answer
 <---------------------------------Other answer <---------------------------------Other answer
So our solution is
 and and 
which can also look like
( , ,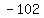 ) )
Notice if we graph the equations (if you need help with graphing, check out this solver)


we get
 graph of graph of  (red) and (red) and  (green) (hint: you may have to solve for y to graph these) intersecting at the blue circle. (green) (hint: you may have to solve for y to graph these) intersecting at the blue circle.
and we can see that the two equations intersect at ( , ,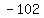 ). This verifies our answer. ). This verifies our answer.
-----------------------------------------------------------------------------------------------
Check:
Plug in ( , ,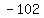 ) into the system of equations ) into the system of equations
Let  and and  . Now plug those values into the equation . Now plug those values into the equation 
 Plug in Plug in  and and 
 Multiply Multiply
 Add Add
 Reduce. Since this equation is true the solution works. Reduce. Since this equation is true the solution works.
So the solution ( , ,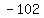 ) satisfies ) satisfies 
Let  and and  . Now plug those values into the equation . Now plug those values into the equation 
 Plug in Plug in  and and 
 Multiply Multiply
 Add Add
 Reduce. Since this equation is true the solution works. Reduce. Since this equation is true the solution works.
So the solution ( , ,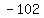 ) satisfies ) satisfies 
Since the solution ( , ,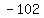 ) satisfies the system of equations ) satisfies the system of equations


this verifies our answer.
|
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) I personally would never solve a pair of equations like this using substitution. When the equations are both in this form ("Ax+By=C"), I would always use elimination.
2x+3y=24
-3x-5y=15
multiply the first equation by 3 and the second by 2 so that the x terms are 6x and -6x; then adding the two equations eliminates x. You can then solve for y, and once you have y you can use either original equation to solve for x.
6x+9y=72
-6x-10y=30
-y=102
y=-102
2x+3(-102)=24
2x-306=24
2x=330
x=165
ANSWER: x=165; y=-102
(2) Solving by substitution, you solve one equation for one variable in terms of the other and substitute that into the other equation.
solve the first equation for x:
2x+3y=24
2x=-3y+24
x=-1.5y+12
substitute that expression for x in the second equation:
-3(-1.5)y+12)-5y=15
4.5y-36-5y=15
-.5y=51
y=51/-.5=-102
x=(-1.5)(-102)+12=153+12=165
Same answer; but the work is a lot uglier....
|
|
|
| |