Question 1190277: A survey of a group of 112 tourists was taken in St louis, the survey showed the following:
62 the Taurus plan to visit gateway Arch;
50 plan to visit the zoo;
11 plan to visit the art museum and the zoo, but not the gateway Arch;
12 plan to visit the art museum and the gateway arch, but not the zoo;
19 plan to visit the gateway Arch and the zoo, but not the art museum;
8 plan to visit the art museum, the zoo, and the gateway Arch;
14 plan to visit none of the three places.
How many plan to visit the art museum only?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A survey of a group of 112 tourists was taken in St Louis, the survey showed the following:
62 the  tourists plan to visit gateway Arch; tourists plan to visit gateway Arch;
50 plan to visit the zoo;
11 plan to visit the art museum and the zoo, but not the gateway Arch;
12 plan to visit the art museum and the gateway arch, but not the zoo;
19 plan to visit the gateway Arch and the zoo, but not the art museum;
8 plan to visit the art museum, the zoo, and the gateway Arch;
14 plan to visit none of the three places.
How many plan to visit the art museum only?
~~~~~~~~~~~~~~
We have a universal set U of 112 tourists (total) and 3 its subsets
A wishing to visit Arch ( n(A) = 62 )
M wishing to visit Museum ( n(M) = ? )
Z wishing to visit Zoo. ( n(Z) = 50 )
We know n(A) = 62,
n(Z) = 50.
We have some info about in-pair intersections of these subsets AM, AZ and MZ, as well as about
their triple intersection AMZ. This info is
n(MZ \ AMZ) = 11,
n(AM \ AMZ) = 12,
n(AZ \ AMZ) = 19,
n(AMZ) = 8.
From this info we have n(MZ) = 11+8 = 19; n(AM) = 12+8 = 20; n(AZ) = 19+8 = 27.
Having it, we can apply the inclusive-exclusive formula (principle), which says
n(A U M U Z) = n(A) + n(M) + n(Z) - n(AM) - n(AZ) - n(MZ) + n(AMZ).
Next, substitute what you just know into the formula. Notice that n(A U M U Z) = 112-14 = 98.
At this moment, we know all the terms in this formula, except of n(M)
98 = 62 + n(M) + 50 - 20 - 19 - 27 + 8, or 98 = 54 + n(M).
From the last equation, we get n(M) = 98 - 54 = 44.
The problem asks us about 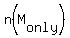 , which is , which is
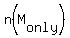 = n(M) - ( n(AM) + n(MZ) - n(AMZ) ) = 44 - (20 + 19 - 8) = 13.
ANSWER. 13 tourists plan to visit the museum only. = n(M) - ( n(AM) + n(MZ) - n(AMZ) ) = 44 - (20 + 19 - 8) = 13.
ANSWER. 13 tourists plan to visit the museum only.
Solved.
--------------------
On inclusion-exclusion principle, see this Wikipedia article
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
To see many other similar (and different) solved problems, see the lessons
- Counting elements in sub-sets of a given finite set
- Advanced problems on counting elements in sub-sets of a given finite set
- Challenging problems on counting elements in subsets of a given finite set
- Selected problems on counting elements in subsets of a given finite set
- Inclusion-Exclusion principle problems
in this site.
Happy learning (!)
|
|
|