SOLUTION: Find the values of x,where 0° < x < 180° such that |2cos x + 3sin x| = sin x

According to the definition of the absolute value, this equation is equivalent to the solution
of this system of equations and inequalities


        if 2cos(x) + 3sin(x) >= 0,  then  2cos(x) + 3sin(x) = sin(x)    (1)

    OR  

        if 2cos(x) + 3sin(x) < 0,  then  2cos(x) + 3sin(x) = -sin(x)    (2).



First, we consider part (1).  So, we should solve

    2cos(x) + 3sin(x) = sin(x).


Simplify it

    2cos(x) = sin(x) - 3sin(x)

    2cos(x) = - 2sin(x)


From this equation, you see that x =/= 90°, so cos(x) can not be zero, and we can divide both sides by 2cos(x). You will get then

    1 = -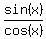,  or tan(x) = -1,  which implies  x = 135°  in the given interval 0° < x < 180°.


Now we should check if the inequality of the part(1)  2cos(x) + 3sin(x) >= 0  is true for x= 135°.

We have cos(135°) = ,  sin(135°) = , therefore

    2cos(x) + 3sin(x) =  +  = , which is positive,

    so we conclude that the part (a) has the solution  x= 135°  in the given interval.



Next, we consider part (2).  So, we should solve

    2cos(x) + 3sin(x) = -sin(x).


Simplify it

    2cos(x) = -sin(x) - 3sin(x)

    2cos(x) = - 4sin(x)


From this equation, you see that x =/= 90°, so cos(x) can not be zero, so we can divide both sides by 2cos(x), You will get then

    1 = -,  or tan(x) = ,  which implies  x = 153.435°  in the given interval 0° < x < 180°.


Now we should check if the inequality of the part(2)  2cos(x) + 3sin(x) <= 0  is true for x= 153.435°.

We have cos(153.435°) = -0.8944,  sin(153.435°) = 0.4472, therefore

    2cos(x) + 3sin(x) = 2*(-0.8944) + 3*0.4472 = -0.4472, which is negative,

    so we conclude that the part (b) has the solution x = 153.435° in the given interval.


ANSWER.  The given equation has two solutions  x = 135°  and  x = 153.435°  in the given interval.