Question 1190085: Write an exponential function in the form y=ab^x
that goes through points (0, 12) and (2,768)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your points are (0,12) and (2,768).
your equation is y = a * b ^ x.
12 is the value of y when x is equal to 0.
you get 12 = a * b^0 which becomes:
12 = a * 1 which becomes:
12 = a.
the equation becomes y = 12 * b ^ x.
y = 768 when x = 2.
the equation becomes 768 = 12 * b^2.
divide both sides of the equation by 12 to get:
64 = b^2.
take the square root of both sides of the equation to get:
64 ^ (1/2) = b
solve for b to get:
b = 8.
the equation becomes y = 12 * 8 ^ x.
that should be it.
this equation can be graphed as shown below:

you can see that, when x = 0, y = 12, and when x = 2, y = 768.
the formula is good for all values of x.
x can be negative or positive.
when x = -1, the formua becomes y = 12 * 8 ^ -1 = 1.5.
the more negative x becomes, the closer to 0 y gets.
y will never, however, be equal to 0.
y = 12 * 8 ^ -30 gets you y = 9.6935 * 10^-27,
that's a very small positive number, but it is not 0.
y will never be 0 nor will y ever be negative.
+
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write an exponential function in the form y=ab^x
that goes through points (0, 12) and (2,768)
~~~~~~~~~~~~~~
In this problem, it is assumed that the parameter b is a positive real number.
First, the problem says that the plot of the function goes through point (0,12).
It means that the value of the function is 12 at x= 0.
So we write 12 = 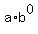 , but since , but since 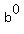 = 1 for any admittable value of b,
it implies that a = 12.
Hence, we can write the function in the form y = = 1 for any admittable value of b,
it implies that a = 12.
Hence, we can write the function in the form y = 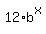 .
Next, the problem says that the plot of the function goes through point (2,768).
It means that the value of the function is 768 at x= 2.
So we write 768 = .
Next, the problem says that the plot of the function goes through point (2,768).
It means that the value of the function is 768 at x= 2.
So we write 768 = 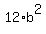 .
Dividing both sides by 12, we get .
Dividing both sides by 12, we get  = =  = 64.
It implies that b = = 64.
It implies that b =  = 8 (we accept positive value of the square root, only).
Finally, the function is y = = 8 (we accept positive value of the square root, only).
Finally, the function is y = 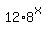 .
You may check, that this function satisfies the imposed conditions. .
You may check, that this function satisfies the imposed conditions.
Solved.
|
|
|