SOLUTION: The current i (in amperes) at time t in a particular circuit is given by i =12sin t + 5cost. Find the maximum current and the first time that it occurs.

Doing it in the Calculus frame, take the derivative 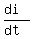 ;  equate it to zero and find the time


The derivative is 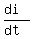  = 12cos(t) - 5sin(t).


The equation 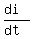  = 0  is  12cos(t) - 5sin(t) = 0,  or  12cos(t) = 5sin(t),  which gives

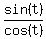     = ,  or  tan(t) = ,


Hence,  t = arctan(12/5) = 1.176 units of time.   It is the first occurrence time of the maximum.     ANSWER



           Since everything happens in the 1st quadrant, 
       where both sin(t) and cos(t) are positive, it is clear
          that the found extremum is indeed the maximum
       (not a minimum), and a special check is not needed.



Next, from tan(t) = ,  we have  sin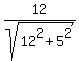(t) =  = ;

                                   cos(t) = .


Substituting these values for sin(t) and cos(t) into the formula for "i", we obtain the value of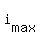  


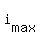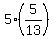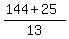     =  +  =  =  = 13 amperes.    ANSWER.