Question 1189691: Hi, please help me out with this question. It is very confusing and I don't know how to approach it.
The tickets for a raffle have four different numbers chosen from 3- 13, with order not important. Determine the probability of winning first prize, which consists of matching all four numbers?
a. 0.3322%
b. 0.3%
c. 29%
d. 0.3030%
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
Hi, please help me out with this question. It is very confusing and I don't know how to approach it.
The tickets for a raffle have four different numbers chosen from 3- 13, with order not important.
Determine the probability of winning first prize, which consists of matching all four numbers?
a. 0.3322%
b. 0.3%
c. 29%
d. 0.3030%
~~~~~~~~~~~~~~~~~
There are 11 numbers 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13.
In all, there are 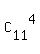 =  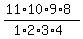= 330 different combinations of 11 items, taken 4 at a time
(330 quadruples).
Only one such combination (quadruple of numbers) provides winning the first prize.
So, the probability is 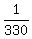 = 0.00303 = 0.3030% (rounded).
ANSWER. Option (d).
Solved.
--------------------
This problem is on COMBINATIONS.
On Combinations, see introductory lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! there are 11 numbers from 3 to 13.
you draw 4 times.
the probability of getting one of the 4 numbers on the first try is 4/11.
the probability of getting one of the remaining 3 numbers on the second try is 3/10.
the probability of getting one of the remaining 2 numbers on the third try is 2/9.
the probability of getting the remaining 1 number on the fourth try is 1/8.
the combined probabiity is 4/11 * 3/10 * 2/9 * 1/8 = .003030303.....
that is equal to .30303030.....%
round that to 4 decimal places to get .3030%.
that would be selection d.
|
|
|
