SOLUTION: If R is a region between the graphs of the function f(x)=sinx and g(x)=cosx over the interval [0,pie] a) find the area of rigion R b)Define R as the region bounded above by the g

Algebra ->  Coordinate Systems and Linear Equations -> SOLUTION: If R is a region between the graphs of the function f(x)=sinx and g(x)=cosx over the interval [0,pie] a) find the area of rigion R b)Define R as the region bounded above by the g      Log On


   

Question 1189664: If R is a region between the graphs of the function f(x)=sinx and g(x)=cosx over the interval [0,pie]
a) find the area of rigion R
b)Define R as the region bounded above by the graph of the function f(x)=root x and below by the graph of the function g(x)=1 over the interval[1,4].find the volume of the solid of the revolution generated by revolving R around the Y-axis.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
No pie in math problems (unless it's a pie chart).
Use the Greek letter pi.

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
If R is a region between the graphs of the function f(x)=sinx and g(x)=cosx over the interval [0,pie]
a) find the area of rigion R
~~~~~~~~~~~~~~~


            In this post,  I will solve problem  (a),  ONLY. 


If you plot the graphs of the functions f(x) = sin(x) and g(x) = cos(x) over the interval [0,pi],

you will see that  g(x) >= f(x)  at 0 <= x <= pi%2F4  and  g(x) <= f(x)  at pi%2F4 <= x <= pi.

Also, you can get it algebraically.



In any case, the area of the region R is the sum of two integrals


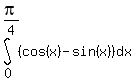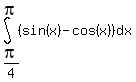    area(R) = int%28%28cos%28x%29-sin%28x%29%29%2C+dx%2C+0%2C+pi%2F4%29 + int%28%28sin%28x%29-cos%28x%29%29%2C+dx%2C+pi%2F4%2C+pi%29.



First integral equals

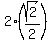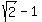    (sin(x) + cos(x))  from 0 to pi%2F4,  which is  2%2A%28sqrt%282%29%2F2%29 - 1 = sqrt%282%29-1%29.



Second integral equals

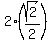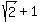    (-cos(x) - sin(x))  from pi%2F4 to pi,  which is  1 + 2%2A%28sqrt%282%29%2F2%29 = sqrt%282%29%2B1.


After adding the integral values, we get

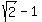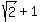    area(R) = sqrt%282%29-1%29 + sqrt%282%29%2B1%29 = 2%2Asqrt%282%29 = 2.828427  (rounded).    ANSWER

Part (a) is solved.