SOLUTION: When organisms die, the amount of carbon-14 in its system starts to decrease. The carbon-14 is about 6000 years. If a piece of human bone was found to contain only 1/3 of carbon-14

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: When organisms die, the amount of carbon-14 in its system starts to decrease. The carbon-14 is about 6000 years. If a piece of human bone was found to contain only 1/3 of carbon-14      Log On


   

Question 1189645: When organisms die, the amount of carbon-14 in its system starts to decrease. The carbon-14 is about 6000 years. If a piece of human bone was found to contain only 1/3 of carbon-14 it originally had, how long ago did the human die
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
When organisms die, the amount of carbon-14 in its system starts to decrease.
The 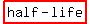highlight%28half-life%29 of the carbon-14 is about 6000 years.
If a piece of human bone was found to contain only 1/3 of carbon-14 it originally had, how long ago did the human die ?
~~~~~~~~~~~~~~~~~~~~ 


The remaining mass M(t) of Carbon-14 is exponentially decreasing function of the time.

According to the problem, the half-life is about 6000 years (5900 years, actually).


So we can write

    M(t) = 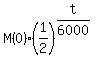M%280%29%2A%281%2F2%29%5E%28t%2F6000%29.


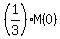We want to find "t", when M(t) = %281%2F3%29%2AM%280%29. So we write the decay equation in the form

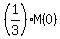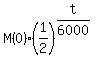    %281%2F3%29%2AM%280%29 = M%280%29%2A%281%2F2%29%5E%28t%2F6000%29.


Our goal is to find "t" from this equation. 


So, we divide both sides by M%280%29, the initial mass of the Carbon-14, and we get

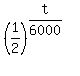    1%2F3 = %281%2F2%29%5E%28t%2F6000%29.


Take logarithm base 10 from both sides

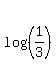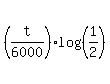    log%28%281%2F3%29%29 = %28t%2F6000%29%2Alog%28%281%2F2%29%29

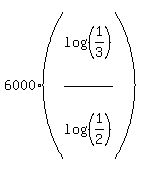    t = 6000%2A%28log%28%281%2F3%29%29%2Flog%28%281%2F2%29%29%29 = 9509.8 years, or 9500 years, rounded.    ANSWER

Solved.

-----------------

On radioactive Carbon-14 dating,  see and learn from the lessons
    - Using logarithms to solve real world problems
    - Radioactive decay problems
    - Carbon dating problems
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Logarithms".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.