Question 1189629: Find the value of (f ∘ g)′ at the given value of x.
f(u)= u/ ((u^2)-1) ,u=g(x)=(6x^2)+x+4, x=0
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the value of (f ∘ g)′ at the given value of x.
f(u)= u/ ((u^2)-1) ,u=g(x)=(6x^2)+x+4, x=0
~~~~~~~~~~~~~~~~~
First, calculations in the post by @MathLover are INCORRECT, since she incorrectly differentiates the fractional function.
So, I came to make everything correctly.
But it is not the only reason why I came.
The entire solution can be done MUCH EASIER, if you not only know the formal definition,
but, in addition, do understand its meaning and are trained to work with it . . .
You do not need to derive many-store long formulas for the composition of functions.
See below, how to make it in a simple way.
The basic formula for the derivative of a composition function is the chain rule
(f o g)'(x) = f'(g(x)) * g'(x).
(1) So, we first calculate g'(x) at the given point x= 0.
(2) Then we calculate g(x) at this point.
(3) Then we derive the formula for f'(u)
(4) Finally, we calculate f'(u) at u = g(x) (substituting the value u= g(x), which we just have calculated in (2) )
Below is my implementation of this procedure.
(1) g'(x) = 2*6*x + 1 = substitute x= 0 to get = 2*6*0 + 1 = 1.
(2) g(0) = (6*0^2) + 0 + 4 = 0 + 0 + 4 = 4.
(3) f'(u) = use the rule of differentiating the fractional function f(u) = 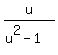 The numerator of the derivative will be 1*(u^2-1) - u*2u = -u^2-1.
We should calculate it at u= g(0) = 4, so the numerator's numerical value is -4^2-1 = -16-1 = -17.
The denominator of the derivative will be (u^2-1)^2.
We should calculate it at u= g(0) = 4, so the denominator's numerical value is (4^2-1)^2 = (16-1)^2 = 15^2 = 225.
(4) Finally, (f o g)'(x) = f'(g(x)) * g'(x) at x= 0 is
The numerator of the derivative will be 1*(u^2-1) - u*2u = -u^2-1.
We should calculate it at u= g(0) = 4, so the numerator's numerical value is -4^2-1 = -16-1 = -17.
The denominator of the derivative will be (u^2-1)^2.
We should calculate it at u= g(0) = 4, so the denominator's numerical value is (4^2-1)^2 = (16-1)^2 = 15^2 = 225.
(4) Finally, (f o g)'(x) = f'(g(x)) * g'(x) at x= 0 is 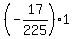 = =  . ANSWER. . ANSWER.
Solved. // All calculations are completed.
---------------
The lesson to learn from my post is THIS :
When you need calculate the value of the derivative of the composite function at given point, do it step by step using the chain rule.
When the component functions are fractional functions, deriving/making the global expression
for the composition first - - - is not the best way, and it DOES NOT FOLLOW to the chain rule.
You can easily make many errors on the way, and you CERTAINLY will do them.
Following the change rule, do as the change rule dictates you:
- (1) first calculate the number g(x0) at given value of x0;
- (2) next find the derivative g'(x0) and evaluate it at the given value of x0;
- (3) next find the derivative f'(u) AS A FUNCTUION of u;
- (4) then evaluate f'(u) at u = g(x0);
- (5) finally, multiplate two numbers f'(g(x0) and g(x0).
That's all.
////////////
Ignore the post by @MathLover1, since it is WRONG BOTH technically and conceptually.
|
|
|