Question 1189622: A girl starts a hike up the mountain at 6 am. 2 hours into the hike she is passed up by a group of people on their way up. At 10 am, the same group of people passes her again on the way down. She finally reached the summit at noon. If the girl and the group of people traveled at constant speeds, at what time did the group reach the summit?
sorry I asked this question yesterday but missed an important part (that she reached the summit at noon).
Found 3 solutions by ikleyn, math_tutor2020, MathTherapy:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A girl starts a hike up the mountain at 6 am. 2 hours into the hike she is passed up by a group of people on their way up.
At 10 am, the same group of people passes her again on the way down. She finally reached the summit at noon.
If the girl and the group of people traveled at constant speeds, at what time did the group reach the summit?
sorry I asked this question yesterday but missed an important part (that she reached the summit at noon).
~~~~~~~~~~~~~~~~~~~~~~~~~
Below is my illustration to the solution.
Let me measure all the distances in kilometers and the rates in kilometers per hour.
--|---------------|---------------|---------------|
<-----
-----> -----> ----->
A B C D
girl passing meeting summit
started point point (the peak)
at 6 am at 8 am at 10 am 12 am for the girl
unknown time for the group
So, according to the problem, the girl and the group started SIMULTANEOUSLY from point B at 8 am
with different rates. Let "u" be the rate of the girl and "v" be the rate of the group.
OBVIOUSLY, u < v. Let d be the distance from B to D, in kilometers.
The girl moved from B to C for 2 hours. So, the distance BC is 2u kilometers.
The group moved from B to D and then back to C for 2 hours, too (the same time).
So, the group covered, in total, the distance 2v in 2 hours, i.e. 2v kilometers.
+---------------------------------------------------------+
| Now it is very important moment for understanding. |
| Track attentively my reasoning. |
+---------------------------------------------------------+
The distance covered by the girl in 2 hours from 8 am to 10 am (BC) PLUS the distance covered
by the group in 2 hours from 8am to 10am (BD + DC) is 2d,
so we can write our first equation 2u + 2v = 2d. (1)
From the other side, d = 4u (2)
since the girl covered this distance BD in 4 hours.
Thus we have two equations, (1) and (2).
To solve the problem, replace 2d in equation (1) by 8u, based on equation (2). Then you get
2u + 2v = 8u,
or
2v = 8u - 2u = 6u.
Hence
v = 6u/2 = 3u.
Thus we obtain that the rate of the group is three times the rate of the girl.
Next, we know that the girl covered BD in 4 hours, from 8 am to 12 am.
Hence, the group spent 1/3 of 4 hours to get the peak, or 1 hour and 20 minutes.
It means that the group reached the peak at 9:20 am.
-------------
Solved.
It is very nice Travel & Distance problem.
\\\\\\\\\\\\\\\\
Comment from student: hi, thank you for the solution, but the problem does not say that they started out at the same time.
it only says that the girl got passed up by the group 2 hours after she started. we only know about the group's
time and distance from that point on.
My response : Your comment told me that you did not understand BOTH the problem and my solution.
The problem SAYS that the group passed the girl at 8 am.
It MEANS that at 8 am they were at the same location at the same time;
hence, we can say that they STARTED from this point simultaneously at 8 am.
What happened before 8 am, DOES NOT MATTER in this problem.
Learn to read, to think and to understand the things correctly . . .
..........................
The level of this problem is much higher than regular problem in Physics at high school.
It is even higher than the level of problems in any college/university for students who are not majoring in Physics
(Chemistry, Biology, Engineering, Psychology, Business administration etc.)
It is the level of leading universities for students majoring in Physics;
it is also the level of Physics circles/(Olympiads in Physics) at high school/college/leading universities - - -
- - - for those students who really want to study Physics at the advanced/professional level.
I know it very well, because I solved MANY similar problems in my time, from more than 10 first-class problems books.
So, the problem is intended for advanced students, who WANT to know MORE - as much as possible,
who see the beauty of Physics and ready to work (to study) on their own, applying as much efforts as it is required.
THEREFORE, when I explain the solution, I see such a student in front of me . . . , and my explanation is intended for such a student.
If I will explain any microscopic detail - such teaching will be USELESS.
So, if you do not understand the solution presented in my post, it simply means that you are in wrong class.
Nevertheless, I am ready to answer any your question, if you have it.
Do not hesitate to ask - - - and happy learning ( ! )
Which high school / college / university / thinking center are you from ?
Which textbook in Physics do you use ?
If you respond (pointing your level, too), I can recommend you some textbooks . . .
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Draw out a number line with these important points- A = the girl's location at 8 AM (the other hikers are here as well; both groups start to travel the same direction)
- B = the girl's location at 10 AM (the hikers are passing the girl in the opposite direction)
- C = the mountain top's location
We don't need to plot the 6 AM location because everything effectively starts at 8 AM.
The girl travels from A to B in 2 hours (8 AM to 10 AM)
The girl travels from B to C in 2 hours (10 AM to 12 PM)
Since she's traveling at the same rate and each segment is the same time duration, this means segments AB and BC are the same length, which I'll call x.
The hiking group travels AB, BC and BC again before meeting up with the girl a second time.
They travel AB+BC+BC = x+x+x = 3x distance units in the same time the girl travels AB = x distance units.
The jump from x to 3x tells us that the hiking group is 3 times faster than the girl.
This must mean that the hiking group takes 1/3 as much time to reach the summit compared to the girl.
It takes the girl 4 hours to reach the summit (from 8 AM to 12 PM) when starting at point A
We take 1/3 of this to get the hiking group's duration
(1/3)*(4 hours) = (1/3)*(240 minutes) = 80 minutes
80 min = 60 min + 20 min = 1 hour + 20 min
The hiking group starts at 8 AM and take 80 minutes (aka 1 hour, 20 min) to reach the top
8:00 AM + (1 hour, 20 min) = 9:20 AM is the final answer.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! A girl starts a hike up the mountain at 6 am. 2 hours into the hike she is passed up by a group of people on their way up. At 10 am, the same group of people passes her again on the way down. She finally reached the summit at noon. If the girl and the group of people traveled at constant speeds, at what time did the group reach the summit?
sorry I asked this question yesterday but missed an important part (that she reached the summit at noon).
Let distance the girl travelled up the mountain be D
Since it took her 6 hours (6:00 a.m. - 12:00 noon) to get to summit, her speed =  When the group passed her at 8:00 a.m. - 2 hours after her departure - she had travelled a distance of
When the group passed her at 8:00 a.m. - 2 hours after her departure - she had travelled a distance of  At 10:00 a.m., or 4 hours into the trip, she’d travelled a distance of
At 10:00 a.m., or 4 hours into the trip, she’d travelled a distance of  When she’d travelled a distance of
When she’d travelled a distance of 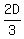 for 4 hours (6:00 a.m. to 10:00 a.m.), the group had travelled a distance
of for 4 hours (6:00 a.m. to 10:00 a.m.), the group had travelled a distance
of  in 2 hours (between meetings, up and down). Therefore, group’s speed = in 2 hours (between meetings, up and down). Therefore, group’s speed = 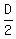 They 1st met at the
They 1st met at the  mark, so at that time, the group had to travel mark, so at that time, the group had to travel 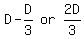 to get to the summit
With the group’s speed being to get to the summit
With the group’s speed being 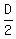 , and as it (the group) travelled a distance of , and as it (the group) travelled a distance of 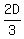 , after meeting her the 1st time, the
group took , after meeting her the 1st time, the
group took  to get to the summit.
Since the group met her 1st, at 8:00 a.m., and took to get to the summit.
Since the group met her 1st, at 8:00 a.m., and took  hours (1 hour, 20 minutes), thereafter, to get to summit, the group reached
the summit 1 hour and 20 minutes after 8:00 a.m., which is hours (1 hour, 20 minutes), thereafter, to get to summit, the group reached
the summit 1 hour and 20 minutes after 8:00 a.m., which is  If this is too complex to follow, then just substitute actual numbers, and it should be quite easy to understand.
If this is too complex to follow, then just substitute actual numbers, and it should be quite easy to understand.
|
|
|