Question 1189594: The mass of a substance, which follows a continuous exponential growth model, is being studied in a lab. The doubling time for this substance was observed to be 23 days. There were 72.6 mg of the substance present at the beginning of the study.
(a) Let t be the time (in days) since the beginning of the study, and let
y be the amount of the substance at time t. Write a formula relating y to t. Use exact expressions to fill in the missing parts of the formula. Do not use approximations.
(b) How much will be present in 8 days?
Do not round any intermediate computations, and round your
answer to the nearest tenth.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula is y = x * e ^ (r * t)
to find the doubling time, let x = 1 and y = 2 and t = 23 days.
the formula becomes:
2 = 1 * e ^ (r * 23)
take the natural log of both sides of the equation to get:
ln(2) = ln(1 * e ^ (r * 23)
since 1 * e = e, the formula becomes:
ln(2) = ln(e ^ (r * 23)
since ln(e ^ (r * 23) = r * 23 * ln(e) and since ln(3) = 1, the formula becomes:
ln(2) = r * 23
divide both sides of the equation by 23 to get:
ln(2) / 23 = r
solve for r to get:
r = .0301368339.
solve for y in the formula to confirm the dobuling time is correct.
you get:
y = 1 * e ^ (.0301368339 * 23) = 2.
this confirms the doubling time is correct.
when the starting value is 72.6, the doubling time will be:
y = 72.6 * e ^ (.0301368339 * 23) = 145.2
since 145.2 is double 72.6, the doubling time is correct when the initial value is 72.6.
when the time from inception if 8 days, then the formula becomes:
y = 72.6 * e ^ (.0301368339 * 8) = 92.39377381.
round this to the nearest 10th to get 92.4
that's your solution.
the formula can be graphed by letting x = t.
here's what the graph looks like.
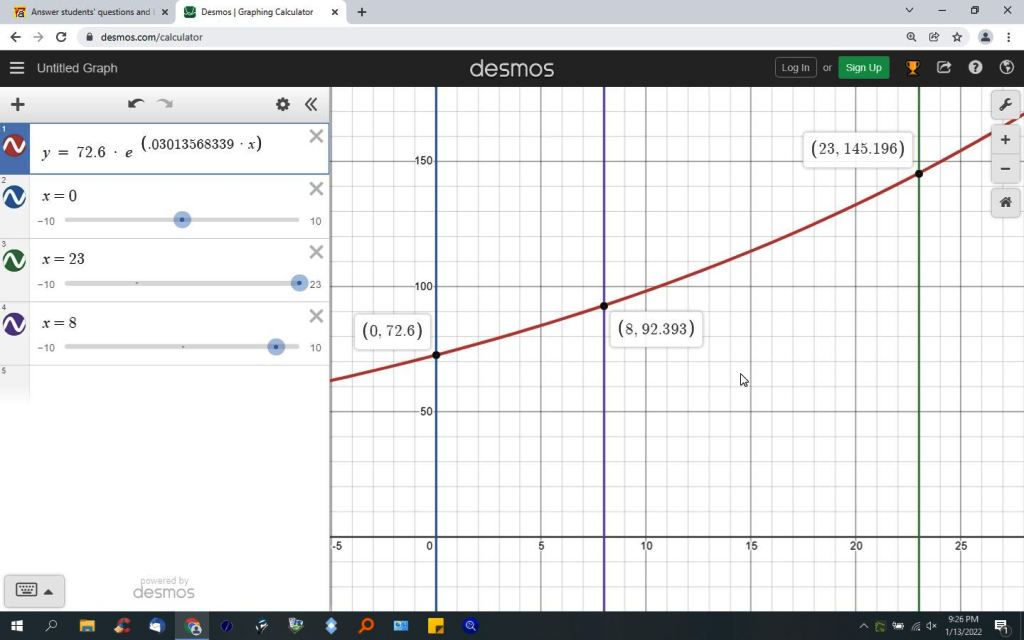
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The mass of a substance, which follows a continuous exponential growth model, is being studied in a lab.
The doubling time for this substance was observed to be 23 days.
There were 72.6 mg of the substance present at the beginning of the study.
(a) Let t be the time (in days) since the beginning of the study, and let
y be the amount of the substance at time t. Write a formula relating y to t.
Use exact expressions to fill in the missing parts of the formula. Do not use approximations.
(b) How much will be present in 8 days?
Do not round any intermediate computations, and round your
answer to the nearest tenth.
~~~~~~~~~~~~~~~~
This problem can be solved in couple of lines with very short simple calculations.
See my solution below.
As the mass is doubling every 23 days, we can write
y = 72.6*2^(t/23), (1)
where t is the time in days. It is LITERAL TRANSLATION of what the problem states.
Formula (1) is the answer to question (a).
To answer question (b), simply substitute t= 8 days into the formula and calculate
y = 72.6*2^(8/23) = use your calculator = 92.39377 milligrams (rounded).
-----------
That is all. The problem is just solved in full.
It is easy and a S T A N D A R D way to solve exponential growth problems,
when the doubling period is given as an input data.
May god save you from making tons unnecessary and nonsensical calculations, which @Theo does in his post.
For peace in your mind, simply ignore his post. It is definitely wrong way to teach.
\\\\\\\\\\\\\\
To see many similar and different solved problems of this kind, look into the lessons
- Population growth problems
- Radioactive decay problems
- Carbon dating problems
- Bacteria growth problems
- A medication decay in a human's body
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|