 @ (1,0)
We need the formula:
@ (1,0)
We need the formula: 
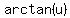

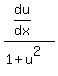 Let
Let  , then
, then  . For the right side,
. For the right side,
 is just a constant and its derivative is 0.
is just a constant and its derivative is 0.
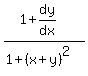

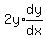 Now we substitute x=1 and y=0, then solve for
Now we substitute x=1 and y=0, then solve for 
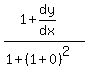

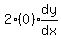
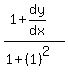


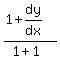


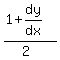


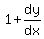




 That's the slope of the tangent line
Now find the equation of the tangent line which goes thru
(1,0), which has the slope m = -1
That's the slope of the tangent line
Now find the equation of the tangent line which goes thru
(1,0), which has the slope m = -1
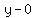

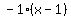


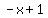
 Edwin
Edwin