|
Question 1189459: For the polynomial Function : F(x)=-2(x + 1/2) (x+4)^3
a)List each real zero and its multiplicity:
b)Determine whether graph crosses or touches the x-axis at each x-intercept:
c)Determine the behavior of the graph near each x-intercept(zero):
d)Determine the maximum number of turning point on the graph:
e)Determine the end behavior, that is finding the power function that the graph of
f resembles for large values of |x|:
Found 2 solutions by MathLover1, Boreal:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For the polynomial Function :

a)List each real zero and its multiplicity:

if  => => ,..... multiplicity 1 ,..... multiplicity 1
if  => => ,..... multiplicity 3 ,..... multiplicity 3
b)Determine whether graph crosses or touches the x-axis at each x-intercept:
For zeros with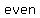 multiplicities, the graphs multiplicities, the graphs 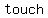 or are tangent to the x-axis at these x-values. or are tangent to the x-axis at these x-values.
For zeros with  multiplicities, the graphs multiplicities, the graphs 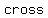 or intersect the x-axis at these x-values. or intersect the x-axis at these x-values.
 have an have an 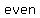 multiplicity => the graph will multiplicity => the graph will 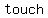 the x-axis the x-axis
 have an have an  multiplicity=> the graph will multiplicity=> the graph will 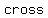 the x-axis the x-axis
c)Determine the behavior of the graph near each x-intercept(zero):
Since the leading term of the polynomial (the term in the polynomial which contains the highest power of the variable) is 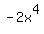 , the degree is , the degree is  , i.e. even, and the leading coefficient is , i.e. even, and the leading coefficient is  , i.e. negative. , i.e. negative.
This means that f(x)→ -∞ as x→ -∞ , f(x)→ -∞ as x→ ∞
d)Determine the maximum number of turning point on the graph:
The maximum number of turning points of a polynomial function is always one less than the degree of the function.
This function f is a  th degree polynomial function and has th degree polynomial function and has  turning points. turning points.
e)Determine the end behavior, that is finding the power function that the graph of
f resembles for large values of | |: |:
If we expand we get

 ..... the dominating term ..... the dominating term
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Graph this:
 ; ; 
By inspection, x=-4 is a root with multiplicity 3, and so is x=-0.5. Both of those make the parentheses 0, and they cross the x-axis.
-
Take the derivative of the function:
f'(x)=2(x+0.5)*3(x+4)^2+(x+4)^3(2)
as x approaches -4 from the either side, the derivative is negative, or the slope negative.
As x approaches 0.5 from either side, the slope is positive.
There is one turning point where the derivative is 0.
2(x+0.5)*3(x+4)^2+2(x+4)^3=0
divide both sides by (x+4)^2
6x+3+2(x+4)=0
8x+11=0
x=-1.375
y=-31.65
-
end behavior negative is (-x)^4 positive oo
and for positive is x^4 positive oo
|
|
|
| |