SOLUTION: A right circular cone with top width 24cm and altitude 8cm is filled with water. A spherical steel ball with radius 3.0cm is submerged in the cone. Find the volume of water below t

Unlike the other tutor, I will assume the ball is heavy 
enough to sink all the way down and touch the sides of 
the cone.  No offense, Greenestamps! lol

Here is the way it looks:



It's easy to see that all 6 right triangles DFC, EFC, OPA, OPB, 
APC, and BPC are similar. Here's a mid-cross-section 



By using the Pythagorean theorem to calculate the hypotenuse CD = 4√(13),
we see that this ratio holds for all 6 right triangles 

shorter leg : longer leg : hypotenuse = 8 : 12 :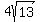 

Dividing through by 4

shorter leg : longer leg : hypotenuse = 2 : 3 : 

Below we will draw the kite ACBO with all the lengths which
we calculate by ratio and proportion of similar triangles
(You don't need to calculate them all).



So the radius of the cone at the bottom (that the sphere "sits in") is 



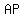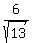and the height of that cone is



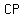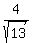We compute its volume by the formula:





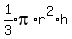
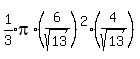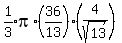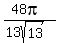However, we see that the volume we want is not the entire cone, because the cone
is "dished out" by the sphere sitting on it.  The "dished out" part is a cap of
the sphere.  So we must calculate the volume of the cap of the sphere which
dishes out the cone, so we can subtract it from the above result.  The formula
for the volume of the cap of a sphere is

 

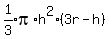where r = radius of the sphere = 3, and 
h = height of the cap.

We calculate the height of the cap, PQ:

PQ = OQ - OP.  OQ is a radius of the sphere, so OQ = 3. So

  

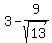So the volume of the cap is



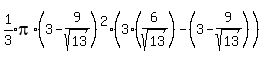That simplifies to 

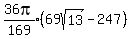So we subtract that from   and get the
volume of water below the sphere as



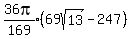which simplifies to:

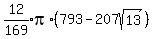 cubic centimeters.

Edwin