Question 1189417: A hot-air balloon is rising vertically at a constant speed, an observer at a distant observes the elevation angle to be 30° at 10:00am, at 10:10am the elevation angle becomes 34°, then at 10:30am the elevation angle of the balloon should be closest (A) 34° (B) 39° (C) 41° (D) 42° (E) 43°
Answer by ikleyn(52794)   (Show Source):
You can put this solution on YOUR website! .
A hot-air balloon is rising vertically at a constant speed, an observer at a distant observes
the elevation angle to be 30° at 10:00am, at 10:10am the elevation angle becomes 34°,
then at 10:30am the elevation angle of the balloon should be closest
(A) 34° (B) 39° (C) 41° (D) 42° (E) 43°
~~~~~~~~~~~~~~~
Let d be the horizontal distance from the observer to the starting point of the balloon.
d is the constant in this problem.
Let h be the height of the balloon. h = h(t) = vt is the linear function of time,
where v is the uniform (=constant) elevation rate in meters per minute.
At 10:00am (the reference time), we have h = tan(30°)*d =  = 0.57735d (the referenced height).
At 10:10am, 10 minutes later, we have h = tan(34°)*d = 0.6745d.
Thus the elevation rate is v = 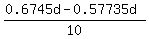 = 0.009715d meters per minute.
At 10:30am, 30 minutes after 10:00am, the elevation will be h = 0.57735d + 30v = 0.57735d + 30*0.009715d = 0.8688d.
At this time, the elevation angle  is  =  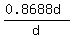= 0.8688.
Hence, = arctan(0.8688) = 40.98 degrees, or 41° (rounded).
ANSWER. Elevation angle will be close to 41°.
Solved.
|
|
|
