Question 1189396: A car engine runs at a temperature of 87°C, when the engine is turned off, it cools according to Newton’s Law of Cooling (T=Ts+D0e-kt) with constant k=0.0347, where the time is measured in minutes. How long does it take for the engine to cool to 33°C if the surrounding temperature is 15°C. (A) 44min (B) 42min (C) 40min (D) 38min (E) 36min (note: ln2=0.6931)
How can i solve this without a calculator?
Found 2 solutions by math_tutor2020, Theo:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given Info:- Ts = surrounding temperature (aka ambient temperature) = 15 degrees C
- T0 = initial temperature of the object = 87 degrees C
- k = 0.0347
- t = time in minutes = unknown and what we want to solve for
- D0 = T0 - Ts = difference in the initial temperature and the surrounding temperature
T = the temperature at time t
uppercase T for temperature, lowercase t for time
The goal is to find lowercase t when uppercase T = 33
T = Ts + D0e^(-kt)
T = Ts + (T0 - Ts)e^(-kt)
33 = 15 + (87 - 15)e^(-0.0347t)
33 = 15 + 72e^(-0.0347t)
33-15 = 72e^(-0.0347t)
18 = 72e^(-0.0347t)
e^(-0.0347t) = 18/72
e^(-0.0347t) = 1/4
Ln( e^(-0.0347t) ) = Ln(1/4)
-0.0347t*Ln(e) = Ln(2^(-2))
-0.0347t = -2*Ln(2)
-0.0347t = -2*0.6931
-0.0347t = -1.3862
t = -1.3862/(-0.0347)
t = 39.9481268011528
t = 40 minutes
All of the calculations shown above are possible to do with pencil & paper only (i.e. without a calculator). It'll take a while, but it's still possible.
Notice that I wrote 1/4 as 2^(-2), and then pulled down the exponent to get Ln(2) term. After which we substitute 0.6931 and evaluate.
Answer: 40 minutes (choice C)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the engine is 87 degrees centigrade when it is shut off.
newton's law of cooling is:
T(t) = Ts + (T0 - Ts) * e ^ -kt.
T(t) is equal to 33 degrees.
T0 is equal to 87 degrees.
Ts is equal to 15 degrees.
the formula becomes:
33 = 15 + (87 - 15) * e ^ (-.0347 * t)
simplify to get:
33 = 15 + 72 * e ^ (-.0347 * t)
subtract 15 from both sides of the equation to get:
18 = 72 * e ^ (-.0347 * t)
divide both sides of the equation by 72 to get:
18/72 = e ^ (-.0347 * t)
take the natural log of both sides of the equation to get:
ln(18/72) = ln(e ^ (-.0347 * t)
by laws of logs, this becomes:
ln(18/72) = -.0347 * t * ln(e).
since ln(e) = 1, this becomes:
ln(18/72) = = -.0347 * t
divide both sides of the equation by -.0347 to get:
ln(18/72) / -.0347 = t
solve for t to get:
t = 39.95084614.
since since 39.95... rounded to 40, your solution is that t = 40 minutes.
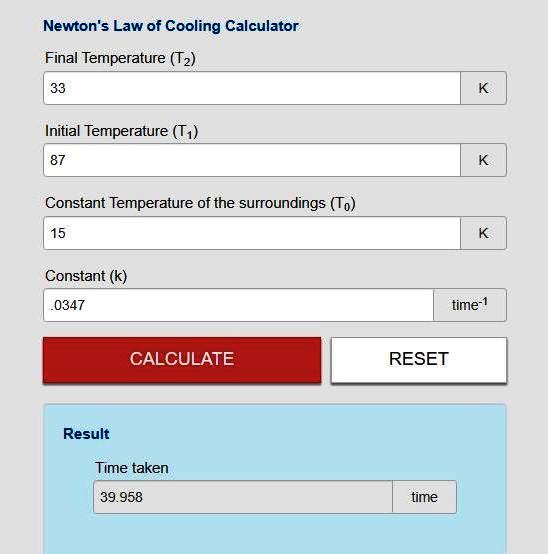
the online calculator at https://www.calctown.com/calculators/newton-law-of-cooling give the same result.
here's a display of the results from using that calculator.
|
|
|