SOLUTION: The complex numbers z and w satisfy |z| = |w| = 1 and zw is not equal to -1. (a) Prove that overline{z} = 1/z and overline{w} = 1/w. (b) Prove that (z + w)/(zw + 1) is a real

Part (a) is the widely known fact. Students learn it on the beginner steps of studying complex numbers.

The proof is very short and straightforward.


Notice, that in part (a), we should prove only first statement for z, since the statement for w is mathematically THE SAME.


    If z = a + bi, then overline(z) = a - bi.

    If |z| = 1, it means that 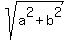 = 1, or, which is the same, a^2 + b^2 = 1.


    Now,   = 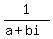 =  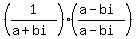=  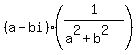= a-bi = overline(z), 

    and the statement is proved.

Part (b) is not widely known, which makes it interesting.


    Since |z| = 1 and |w| = 1, it means that z and w are the unit vectors of the length 1: their endpoints lie on the unit circle.

    To calculate (z+w), apply the parallelogram's rule.  Since the sides of the parallelogram on vectors z and w are equal,

    the parallelogram is a rhombus.  The sum (z+w) is the diagonal of the parallelogram, and since parallelogram is a rhombus,

    arg(z+w) is  EITHE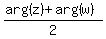R   OR  .   Here arg() means the argument of complex number.



    The first case   arg(z+w) = 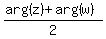 is when the angle between vectors z and w is less than  :  |arg(z)-arg(w)| <= .

    The second case  arg(z+w) = 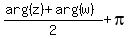 is when the angle between vectors z and w is greater than  :  |arg(z)-arg(w)| > .

    Notice that by the modulo of ,  arg(z+w) = 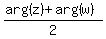   always.



    Further, the product zw is the unit vector, again, so the same formulas are applicable to vectors zw and 1 = (1,0).

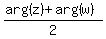    Notice that arg(zw) = arg(z) + arg(w), so arg(zw+1) is EITHER ,  or  , depending
    on the angle between vectors zw and 1 = (1,0).

    But in any case,  the vectors (z+w) and (zw+1) are EITHER parallel OR anti-parallel (opposite).

    By the modulo of ,  arg(zw+1) = 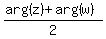   always.



    By the rule of argument of quotient for complex numbers, it means that the ratio 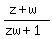  is real number.

    This real number is EITHER positive (when the vectors (z+w) and (zw+1) are parallel), 

                          OR   negative (when the vectors (z+w) and (zw+1) are anti-parallel).