|
Question 1189278: A jar contains red, white, and yellow candy pieces
in the ratio 9:5:4 of respectively. When 7 pieces of red
candy and 5 pieces of white candy are removed
from the jar and 3 pieces of yellow candy are added,
the ratio of red to white to yellow becomes 4: 2: 3.
If the jar contains only these three colors of candy,
how many pieces were originally in the jar?
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
A jar contains red, white, and yellow candy pieces
in the ratio 9:5:4 of respectively. When 7 pieces of red
candy and 5 pieces of white candy are removed
from the jar and 3 pieces of yellow candy are added,
the ratio of red to white to yellow becomes 4: 2: 3.
If the jar contains only these three colors of candy,
how many pieces were originally in the jar?
~~~~~~~~~~~~~~~~~~
From the condition, we can write
R = 9x, W = 5x, Y = 4x
for the number of red, white and yellow candy pieces in the jar originally,
where x is the common factor (multiplier).
According to the condition, we have this proportion
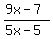 =  = 2,
which gives
9x - 7 = 2*(5x-5)
9x - 7 = 10x - 10
10 - 7 = 10x - 9x
x = 3.
At this point, we can just answer the problem's question: R = 27, W = 15, Y = 12.
The last condition is EXCESSIVE, and we should check that it does not contradict to
(is consistent with) the answer.
CHECK. After manipulations, the jar contains R = 20, W = 10 and Y = 15 candy pieces,
so this proportionality 4 : 2 : 3 is held for the final state.
Solved and explained.
|
|
|
| |
