Question 1189249: A factory sorts pencils into bags such that 19 large bags plus 3 small bags contain a total of 224 pencils. The sum of the number of pencils in a large bag plus the number in a small bag is:
A)16 B)36 c)42 D)19 E)18
Found 4 solutions by greenestamps, Solver92311, math_tutor2020, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let x be the number of pencils in a large bag; let y be the number in a small bag. Since the total number of pencils is 224, we have
19x+3y=224
where x and y have to be positive integer values.
We can solve the problem informally, using trial and error. The total of 224 pencils, minus the number of pencils in the 19 large bags, equals the number of pencils in the 3 small bags; that means the number of pencils in the small bags is a multiple of 3.
So try some numbers....
10 pencils in each large bag makes 19*10=190 pencils, leaving 224-190=34 pencils in the small bags. But 34 is not a multiple of 3. So try something else.
11 pencils in each large bag makes 19*11=209 pencils, leaving 224-209=15 pencils in the small bags. 15 IS a multiple of 3: 3*5=15.
So we have one POSSIBLE solution: 11 pencils in each large bag and 5 pencils in each small bag.
Technically, we need to verify that this is the only solution. However, I will leave that part for the formal algebraic solution below.
But for now, we have....
(One possible) ANSWER: The sum of the numbers of pencils in a large bag and in a small bag is 11+5 = 16.
While a problem like this can be solved informally, it is useful to know the formal mathematical method.
This is a Diophantine equation -- a problem in which we have two variables but only one equation; but we can find the solution (or possible a family of discrete solutions) knowing that the values of the variables are non-negative integers.
Here is the standard method for solving a linear Diophantine equation like in this problem.
Our equation is

Step 1: Solve the equation for one variable in terms of the other. You should be able to finish solving the problem by solving for either variable. I will show the solution solving for y in terms of x.

Isolate the y term:

When we divide by 3, we want to express as much of the result as possible in whole numbers. In this problem, it might look like this:


In that equation, we know y is an integer, and x is an integer so (-7x+74) is an integer; and that means  must be an integer. must be an integer.
Since 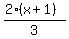 must be an integer, (x+1) must be a multiple of 3, so the possible values of x are 2, 5, 8, 11, .... must be an integer, (x+1) must be a multiple of 3, so the possible values of x are 2, 5, 8, 11, ....
We look at those possible values of x and find the one(s) that make y a positive integer:
x y=(-7x+74)+(2(x+1)/3)
--------------------------
2 (-14+74)+2 = 60+2 = 62
5 (-35+74)+4 = 39+4 = 43
8 (-56+74)+6 = 18+6 = 24
11 (-77+74)+8 = -3+8 = 5
14 (-98+74)+10 = -24+10 = -14
We see that, mathematically, there are several ways to get 224 pencils with 19 large bags and 3 small bags:
(1) 2 in each large bag and 62 in each small bag: 19(2)+3(62)=38+186=224
(2) 5 in each large bag and 43 in each small bag: 19(5)+3(43)=95+129=224
(3) 8 in each large bag and 24 in each small bag: 19(8)+3(24)=152+72=224
(4) 11 in each large bag and 5 in each small bag: 19(11)+3(5)=209+15=224
However, in the context of the problem, there should be more pencils in a large bag than in a small bag; that leaves only one solution: 11 pencils in each large bag and 5 in each small bag.
ANSWER: (formally) There are 11 pencils in each large bag and 5 in each small bag
Answer by Solver92311(821)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are some great answers already. I'll post a different viewpoint.
L = number of pencils in one large bag
s = number of pencils in one small bag
3s = number of pencils from the three small bags only
19L = number of pencils from the 19 large bags only
19L+3s = number of pencils total from all bags mentioned
19L+3s = 224
This is one of the equations in the system.
The goal is to find the number k such that L+s = k
We're given five possible answer choices: {16,36,42,19,18}. The value k takes on one of those numbers.
If k = 16, then we have this system

Solving that system leads to (L,s) = (11,5)
So this is one possible solution.
If k = 36, then we have this system

Solving that system leads to (L,s) = (7.25,28.75)
We can rule this out because L and s must be positive whole numbers.
If k = 42, then we have this system

Solving that system leads to (L,s) = (6.13,35.88)
This can be ruled out for similar reasoning as above.
If k = 19, then we have this system

Solving that system leads to (L,s) = (10.44,8.56)
This can be ruled out for similar reasoning as above.
If k = 18, then we have this system

Solving that system leads to (L,s) = (10.63,7.38)
This can be ruled out for similar reasoning as above.
In short, choices B through E can be ruled out because they lead to L & S being nonwhole decimal numbers. Only choice A is valid.
I skipped the steps in solving each system, so let me know if you need to see those steps.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A factory sorts pencils into bags such that 19 large bags plus 3 small bags contain a total of 224 pencils.
The sum of the number of pencils in a large bag plus the number in a small bag is:
A)16 B)36 c)42 D)19 E)18
~~~~~~~~~~~~~~
Now, when you have so many solutions from different tutors, it should be clear
that the true challenge is to get short, straightforward and convincing solution.
Consider this one below.
Let x be the number of pencils in a large bag and y be the number of pencils in a small bag.
Then you have this equation
19x + 3y = 224 (1)
and this inequality
x > y (2)
Equation (1) should be solved in whole numbers.
Inequality (2) is the math translation of the terms "large bag" and "small bag".
Using inequality (2), we get the following inequality from equation (1)
19x + 3x > 224, or 22x > 224,
It gives x > 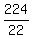 = 10.1818..., and since x should be whole number, it implies x >= 11.
So, we need find the solution to equation (1) in whole numbers x, y with x >= 11.
There are not so many such possibilities: 19*11 = 209 and 19*12 = 228,
so the only real candidate is x = 11.
It gives y = = 10.1818..., and since x should be whole number, it implies x >= 11.
So, we need find the solution to equation (1) in whole numbers x, y with x >= 11.
There are not so many such possibilities: 19*11 = 209 and 19*12 = 228,
so the only real candidate is x = 11.
It gives y = 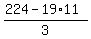 = = 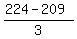 = =  = 5, which is a whole number.
So, the problem has a UNIQUE solution x= 11, y= 5, which gives the sum x + y = 11 + 5 = 16.
ANSWER. The number of pencils in a large bag plus the number in a small bag is 16 (option (A) ). = 5, which is a whole number.
So, the problem has a UNIQUE solution x= 11, y= 5, which gives the sum x + y = 11 + 5 = 16.
ANSWER. The number of pencils in a large bag plus the number in a small bag is 16 (option (A) ).
Solved.
|
|
|