Question 1189105: A test to detect cancer is not always reliable. It gives a positive result 95 % of the time if the person does have cancer, and it gives a positive result 3 % of the time that the person does not. The probability that a randomly selected person has cancer is 0.02.
a. Given that a test on a randomly selected person is positive, find the probability that he/she does have cancer? Ans: 0.393
b. Out of 5000 people on which this test is used, how many people with cancer would you expect to be correctly diagnosed? Ans: 95 people
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! ===TP======TN======Total
CA+190=====10=======200
CA-294====9506======9800
total 484===95216======10000
I picked 1000 at random, and the table can be filled out.
So positive test (484),probability of cancer is 190/484=0.393
-
===TP======TN======Total
CA+95=====5=======. 100
CA-147====4753======4900
total 242===4758======5000
upper left corner shows 95 TP/Ca+
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A test to detect cancer is not always reliable.
It gives a positive result 95 % of the time if the person does have cancer,
and it gives a positive result 3 % of the time that the person does not.
The probability that a randomly selected person has cancer is 0.02.
a. Given that a test on a randomly selected person is positive,
find the probability that he/she does have cancer? Ans: 0.393
b. Out of 5000 people on which this test is used, how many people with cancer
would you expect to be correctly diagnosed? Ans: 95 people
~~~~~~~~~~~~~~~
PART (a)
Consider a population of 100,000 people.
Of them, 0.02 have cancer, i.e. 0.02*100,000 = 2000, according to the problem.
Of these 2000, 95% will have a true positive test, i.e. 1900 persons.
Of the remaining 100,000-2,000 = 98,000 people, 3% will have a false positive test, i.e. 2940 persons.
In all, of 100,000 population, 1900 + 2940 = 4840 have positive cancer test.
The ratio 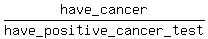 = = 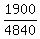 = 0.393, rounded.
It is the answer to question (a), deduced informally.
Formally, it is P = = 0.393, rounded.
It is the answer to question (a), deduced informally.
Formally, it is P = 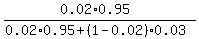 = 0.393 (rounded). = 0.393 (rounded).
|
|
|