Question 1189075: In a raffle, 1800 tickets are sold. 3 prizes will be given starting with 3rd prize, then second, then first. A person buys 16 tickets which are all eligible to win prizes. What are the odds of this person winning the top two prizes?
Found 2 solutions by Solver92311, ikleyn:
Answer by Solver92311(821)   (Show Source): (Show Source):
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a raffle, 1800 tickets are sold. 3 prizes will be given starting with 3rd prize, then second, then first.
A person buys 16 tickets which are all eligible to win prizes.
What are the odds of this person winning the top two prizes?
~~~~~~~~~~~~~~~~~
With this problem/post, I am in difficult position :
I need to write long explanation.
First of all, the problem is posed INCORRECTLY.
(1) A standard lottery does not work in a way described in the post.
A standard lottery HAS NO priority in the order of winning prizes.
The prize is won, if the number on the ticket coincides with the number given to the prize by the lottery machine.
If the specific lottery works differently (as worded in the post), it must be thoroughly / carefully reflected
in the description, which is not done in the post.
(2) The question is posed in a way, which makes it unclear.
What is "winning the top two prizes" ? - - - Are they the 1st and the 2nd, only ?
Or the 3rd and the 2nd, only ? - - - Or any two of the top three prizes ?
(3) How the problem is worded, it makes it clear, that the problem formulation is not professional
and is ambiguous.
It means that the problem came not from a peer-reviewed textbook: it is created by an unprofessional amateur,
or recovered from an UNTRUSTED source.
(4) Regarding such posts, my position is that they do not deserve a professional consideration, AS A RULE.
My position is that at this forum we, the tutors, teach the students / (the visitors) to solve correctly
posed mathematical problem, but we do not teach unprofessional "problems' composers" to create their
problems. These two activities (teaching to solve and teaching to create Math problems) are two
absolutely distinct areas with zero intersection.
Similar as in music performing and composing are two distinct activities, requiring different skills.
(4b) There are exclusions from this my rule. One possible exclusion is when the problem is outstandingly
nice (at least, potentially) or the solution is outstandingly educative (at least, potentially).
But this problem is a standard; it is difficult to consider it as outstanding.
(5) Therefore, my standard position relating to such posts is EITHER ignore them, or EXPLAIN to the visitor
that it is posed incorrectly, or TO DELETE such post/(posts) to avoid unnecessary and unproductive
explanations/discussions.
So, my choice was between ignoring, explaining or deleting . . .
(6) But this case now became special. It became special because the other tutor before me published INCORRECT SOLUTION.
Now my concern is not about the visitor, who posted the problem (everything is clear to me about him . . . )
My concern is about those future readers and next generations of students, who (probably) will read these
related solutions from the archive.
They should be confident that the tutors of this forum (as an entire body) are able to read, to solve and to understand
the problems correctly and to interpret them adequately.
+---------------------------------------+
| It is WHY I WRITE THESE LINES. |
+---------------------------------------+
(7) So, I will consider the problem in this REFORMULATED form
In a raffle, 1800 tickets are sold. 2 prizes will be given, the 1st and the 2nd.
A person buys 16 tickets. What are the odds of this person winning the top two prizes?
As I explained above, it is not the only possible interpretation of the problem.
Another interpretations are possible.
But I chose this one BECAUSE the other tutor solved it incorrectly in this formulation.
So, see my correct solution below.
(8) The probability to win two prizes, having 16 tickets bought, is
P = 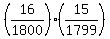 = reduce fractions = = reduce fractions = 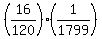 = = 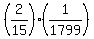 = = 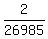 .
It means that the odds of this person in favor of winning the top two prizes are 2 against 26985-2 = 26983.
ANSWER. The odds of this person in favor of winning the top two prizes are 2 against 26983. .
It means that the odds of this person in favor of winning the top two prizes are 2 against 26985-2 = 26983.
ANSWER. The odds of this person in favor of winning the top two prizes are 2 against 26983.
Solved, answered and explained.
|
|
|