SOLUTION: If a sphere has a radius of 6cm rests on 3 horizontal wires forming a plane triangle whose sides are 5cm, 12cm, and 13cm. Find the height of the top of the sphere above the plane o

The plane of triangle cuts the sphere, and the section is the circle inscribed in the triangle.


For any triangle, the radius of the inscribed circle is the area of the triangle divided by its semi-perimeter

    r = .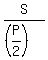


In our case, the triangle is right-angled (the triple 5,12,13 is the Pythagorean triple), 

so its area is half the product of its legs S = 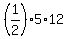 = 30 cm^2.


The perimeter of the triangle is  P = 5 + 12 + 13 = 30 cm.


So, the radius of the inscribed circle is r = 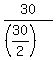 = 2 cm.


Hence, the distance from the center of the sphere to the cutting plane is 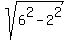  = 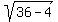 =  =  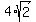cm.


The top of the sphere above the cutting plane is  6 +  = 11.657 cm (rounded).    ANSWER