SOLUTION: Hello all, could you please help me with this problem? Would greatly appreciate the help. <a rel=nofollow HREF="https://imgbb.com/"><img src="https://i.ibb.co/SKYyCNx/IMG-6263.j

Since the shown angles are equal, the shown segments inside triangle are bisectors of respective angles.


    +----------------------------------------------------------------------+
    |    In any triangle, bisector of an angle divides the opposite side   |
    |        in the ratio equal to the ratio of adjacent sides.            |
    +----------------------------------------------------------------------+


THEREFORE, in the given triangle 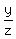  =   and  y + z = 5.

    So, the side of the length 5 is divided in the ratio 6:4.

    It means that y = 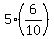 =  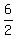= 3;  z = 5-3 = 2.



Similarly, side of the length 6 is divided in propoprtion   = .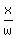

    So, the side of the length 6 is divided in the ratio 5:4.

    It means that  x = 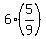 =  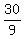=  = 3 ,  w = 6 - 3  = 2 .


ANSWER.  x = 3 ;  y = 3;  z = 2;  w = 2 .