SOLUTION: The smallest positive number for which 3sin(2x−6)=1 Hint: Proceed as in the preceding problem to find some solution of the equation. Then look for the smallest positive.

We transform given equation this way

    sin(2x-6) = 1/3


After that, we get two possible forms

         (a)  2x-6 = arcsin(1/3) + 2k*pi

    and

         (b)  2x-6 = pi - arcsin(1/3) + 2k*pi


It gives two expressions for x

         (a)  x = (arcsin(1/3) + 6)/2 + k*pi
        
    and

         (b)  x = (pi - arcsin(1/3) +6)/2 + k*pi


Giving values  k= 0 and -1 for(a)  and  k=0 and -1 for (b), we get 4 values for x in the interval [0,2pi), in radians


    1)  x = 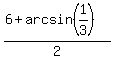 =  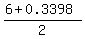= 3.169918455,


    2)  x = 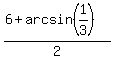 -  =  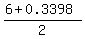-  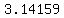= 0.028328455,


    3)  x = 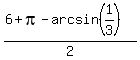 =  = 4.400876545,


    4) 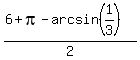  -  =  -  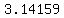 = 1.259286545.


The minimum of these 4 values is  0.028328455.     ANSWER