.
A city council voted to conduct a study on inner-city community problems. A nearby university was contacted to provide
a maximum of 40 sociologists and research assistants.
Each sociologist will spend 10 hours per week collecting data in the field and 30 hours per week
analyzing data in the research center.
Each research assistant will spend 30 hours per week in the field and 10 hours per week in the research center.
The minimum weekly labor-hour requirements are 280 hours in the field and 360 hours in the research center.
The cost per week for each sociologist and research assistant are Php 5000 and Php 3000 respectively.
A. How many sociologists and research assistants should be hired to meet the weekly labor hour requirements
and minimize the weekly cost? What is the weekly cost?
B. Repeat part A if the council decides that they should not hire more sociologists than research assistants.
~~~~~~~~~~~~~~~
Part (A).
Let x be the number of sociologists; y be the number of research assistances.
From the problem, the condition to minimize the weekly cost is to satisfy these two equations
10x + 30y = 280 (1) (hours in the field)
30x + 10y = 360 (2) (hours in the research center)
These are the only restrictions in the problem part (A); there are NO other restrictions in Part (A).
Canceling the common factor 10 in both equations, you get the simplified equations
x + 3y = 28 (1)
3x + y = 36 (2)
Solve by using the determinants
x = 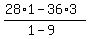 =
=  = 1; y =
= 1; y = 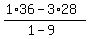 = 6.
So, the ANSWER for part (A) is: 1 sociologist and 6 research assistances.
The minimum weekly cost then is 1*5000 + 6*3000 = 23000 pesos.
= 6.
So, the ANSWER for part (A) is: 1 sociologist and 6 research assistances.
The minimum weekly cost then is 1*5000 + 6*3000 = 23000 pesos.
Part (A) is solved.
Part (B).
The solution/(answer) to Part (A) satisfies the requirements of Part (B), so the
ANSWER for part (B) is the same, as for part (A).
Solved.