|
Question 118890: I HAVE NOW HAD PRACTICE SOLVING EQUATIONS WITH ONE VARIABLE AND EQUATIONS WITH TWO VARIABLES. Comparing equations with one variable to equations with two variables. How are they alike? How are they different? and what if an equation had three variables?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
the general rule for solving this kind of equations is:
if you have to find 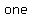 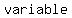 you need you need 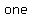 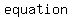
if you have to find  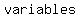 you need you need  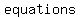
if you have to find  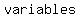 you need you need 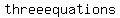
:and so on
:
:
if you have to find  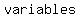 you need you need  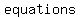
If you compare of equations with and and  variables, they have similarities such as: variables, they have similarities such as:
both of them have  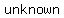 number, which you need to get number, which you need to get
in order to do it, you will need to use algebraic 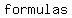 , , 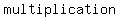 , ,  , , 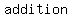 , or , or 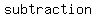
The  between them is making between them is making 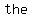  in which they are treated to get the unknown number. in which they are treated to get the unknown number.
Many problems can be solved quickly and easily using 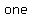  with with 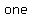 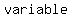 . .
Other problems that might be difficult to solve in terms of 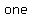 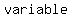 can easily be solved using can easily be solved using  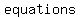 and and  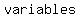 . .
the following example shows the difference in the  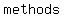 ; solved first by using one variable and then using two: ; solved first by using one variable and then using two:
1. method
Find the two numbers such that half the first equals a third of the second and twice their sum exceeds three times the second by  . .
 is first number is first number
Then
 of the second number
=> of the second number
=> 
 .multiply both sides by
.multiply both sides by 
 .
.
 .
.
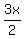 .is second number
.is second number
twice their sum exceeds three times the second by 


 multiply both sides by
multiply both sides by 



 is first number
is first number
 .
.
 is second number is second number
2. method
If we let  and and  be the first and second numbers, respectively, we can write be the first and second numbers, respectively, we can write  equations: equations:
 .(1)
.(1)
 .(2)
.(2)
now solve for  first equation, and substitute this value in the second: first equation, and substitute this value in the second:



 .(2)
.(2)
 multiply both sides by
multiply both sides by 








|
|
|
| |