|
Question 1188897: Please help me solve this.
A city council voted to conduct a study on inner-city community problems. A nearby university was contacted to provide a maximum of 40 sociologists and research assistants. Each sociologist will spend 10 hours per week collecting data in the field and 30 hours per week analyzing data in the research center. Each research assistant will spend 30 hours per week in the field and 10 hours per week in the research center. The minimum weekly labor-hour requirements are 280 hours in the field and 360 hours in the research center. The cost per week for each sociologist and research assistant are Php 5000 and Php 3000 respectively.
A. How many sociologists and research assistants should be hired to meet the weekly laborhour requirements and minimize the weekly cost? What is the weekly cost?
B. Repeat part A if the council decides that they should not hire more sociologists than research assistants.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! (a)
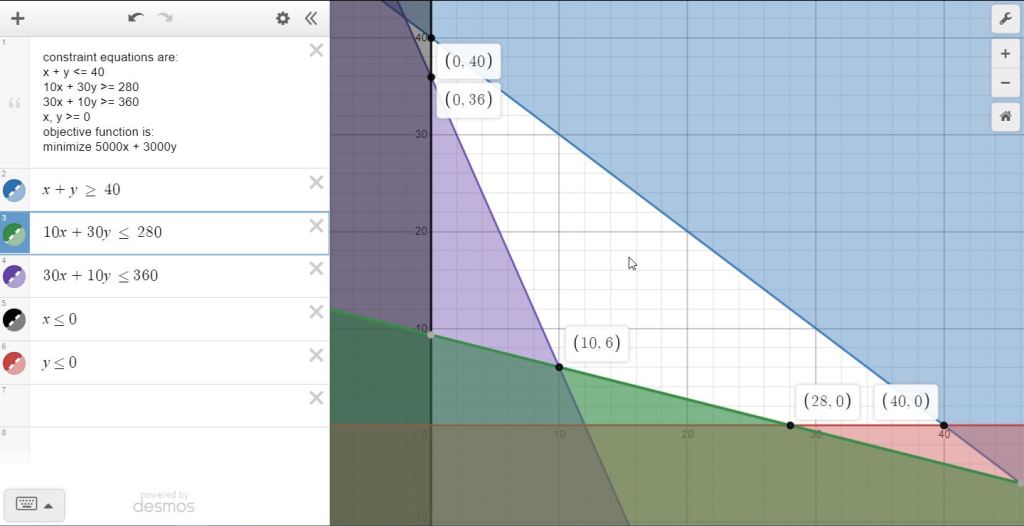
constraint equations are:
x + y <= 40
10x + 30y >= 280
30x + 10y >= 360
x, y >= 0
objective function is:
minimize 5000x + 3000y
(b)
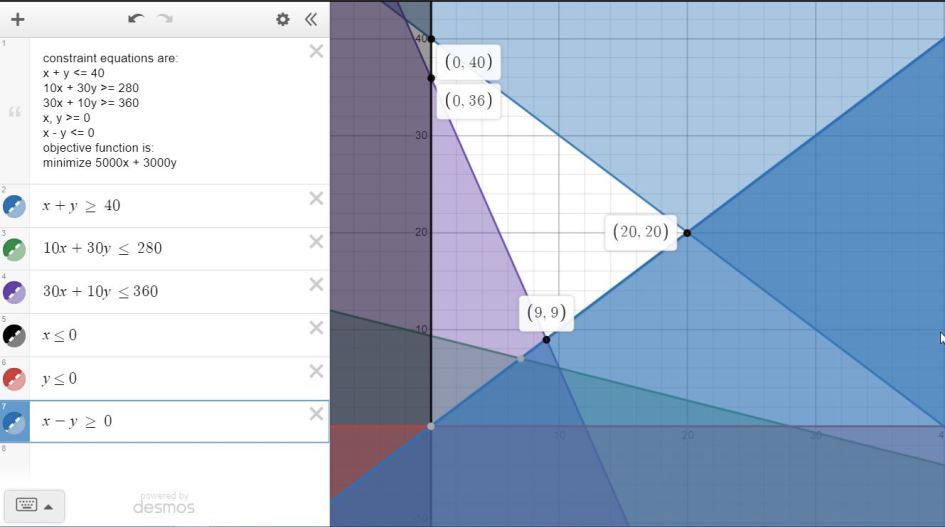
constraint equations are:
x + y <= 40
10x + 30y >= 280
30x + 10y >= 360
x, y >= 0
x - y <= 0
objective function is:
minimize 5000x + 3000y
(b) is the same as (a) but with the additional requirement that x <= y.
if you subtract y from both sides of this inequality, you get x - y <= 0.
the graphical analysis a and the simplex tool analysis both indicate that:
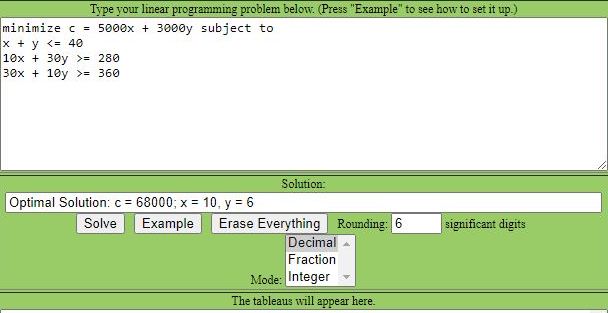
minimum cost for (a) is 68,000.
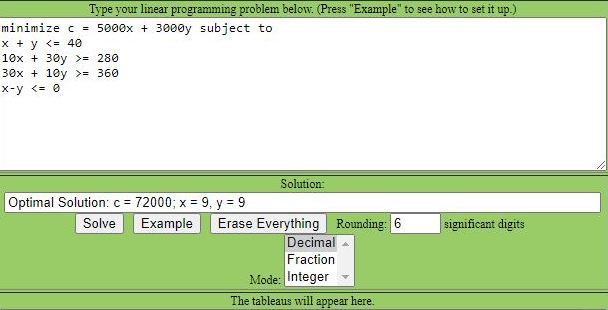
minimum cost for (b) is 72,000
for (a) at (10,6), the constraint are:
x + y <= 40 = 10 + 6 <= 40 which is true.
10x + 30y >= 280 = 10*10 + 30*6 >= 280 = 280 >= 280 which is true.
30x + 10y >= 360 = 10*30 + 6*10 >= 360 = 360 >= 360 which is true.
x >= 0, y >= 0 which is true.
for (b) at (9,9), the constraints are:
x + y <= 40 = 9 + 9 <= 40 = 18 <= 40 which is true.
10x + 30y >= 280 = 10*9 + 30*9 >= 280 = 360 >= 280 which is true.
30x + 10y >= 360 = 30*9 + 10*9 >= 360 = 360 >= 360 which is true.
x >= 0, y >= 0 which is true.
x - y <= 0 = 9 - 9 <= 0 = 0 <= 0 which is true.
all the constraints are met for both (a) and (b) at the minimum cost point.
for (a), the minimum cost point is (10,6).
for (b), the minimum cost point is (9,9).
for (a), the results are shown below, first for the graphical analysis and next for the simplex tool analysis.
for (b), the results are shown below, first for the graphical analysis and next for the simplex tool analysis.
with the graphical analysis, using the desmos.com calculator, you are graphing the opposite of the constraint inequalities.
the area of the graph that is not shaded is the feasible region.
the minim cost will be at the corner points of the feasible region, as shown.
you evaluate the objective function at each of the corner points to find the corner point that has the minimum cost.
with the simplex tool, you need to make each inequality have the variables on the left and the constant on the right.
that is why x <= y had to be shown as x - y <= 0.
the problem statement is a little unrealistic because it allowed for 0 sociologist or 0 research assistants.
this would not be a possible combination in a realistic environment where you would need at least some sociologists and some research asistants.
despite that, the minimum cost solution did include some sociologists and some research assistants.
Answer by ikleyn(52776)   (Show Source): (Show Source):
|
|
|
| |