SOLUTION: {{{a+4 divided by 3a^3+10a^2-5a+12}}}. I have tried it and I can only get to the second variable. I have gone on to the next question and then gone back to it more than once.

Click here to see ALL problems on Expressions-with-variables

Question 118875: .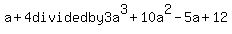
I have tried it and I can only get to the second variable.
I have gone on to the next question and then gone back to it more than once.
Found 2 solutions by stanbon, jim_thompson5910:
Answer by stanbon(75887) (Show Source):
You can put this solution on YOUR website!
a+4 divided by 3a^3+10a^2-5a+12
-----------
I think you want to divide the cubic by a+4.
If you use synthetic division yu get the following:
----------------------------
-4....3....10,,,,-5,,,,12
.......3....-2.....3....|..0
Remainder: zero
Quotient: 3x^2-2x+3
======================
Cheers,
Stan H.

Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website!
Note: I'm going to use "x" instead of "a"

Let's simplify this expression using synthetic division

Start with the given expression

First lets find our test zero:

Set the denominator equal to zero

Solve for x.

so our test zero is -4

Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.

-4 | 3 10 -5 12
|

Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 3)

-4 | 3 10 -5 12
|
3

Multiply -4 by 3 and place the product (which is -12) right underneath the second coefficient (which is 10)

-4 | 3 10 -5 12
| -12
3

Add -12 and 10 to get -2. Place the sum right underneath -12.

-4 | 3 10 -5 12
| -12
3 -2

Multiply -4 by -2 and place the product (which is 8) right underneath the third coefficient (which is -5)

-4 | 3 10 -5 12
| -12 8
3 -2

Add 8 and -5 to get 3. Place the sum right underneath 8.

-4 | 3 10 -5 12
| -12 8
3 -2 3

Multiply -4 by 3 and place the product (which is -12) right underneath the fourth coefficient (which is 12)

-4 | 3 10 -5 12
| -12 8 -12
3 -2 3

Add -12 and 12 to get 0. Place the sum right underneath -12.

-4 | 3 10 -5 12
| -12 8 -12
3 -2 3 0

Since the last column adds to zero, we have a remainder of zero. This means is a factor of

Now lets look at the bottom row of coefficients:

The first 3 coefficients (3,-2,3) form the quotient

So

You can use this online polynomial division calculator to check your work