.
The center of a hyperbola with equation 9x2 - 25y2 - 225 = 0 is moved 5 units to the right and 2 units down.
Find the equation in standard form of the hyperbola in its new position.
~~~~~~~~~~~~~~
Starting from the given equation, divide its both sides by 225.
You will get then the hyperbola equation in the standard form
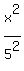 -
- 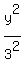 = 1.
The center of this (given) hyperbola is the origin of the coordinate system (o,o).
After described translations, the center of the new hyperola is at the point (5,-2).
THEREFORE, the standard equation of the translated hyperbola is
= 1.
The center of this (given) hyperbola is the origin of the coordinate system (o,o).
After described translations, the center of the new hyperola is at the point (5,-2).
THEREFORE, the standard equation of the translated hyperbola is
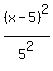 -
- 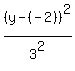 = 1,
or, which is the same, but simpler
= 1,
or, which is the same, but simpler
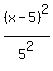 -
-  = 1. ANSWER
= 1. ANSWER
Solved.